点击我爱计算机视觉标星,更快获取CVML新技术
是 LAB 针对前端智能设备开发的软件开发包,核心部分是一个轻量级,模块化,高性能的AI 推断引擎,并支持用DLA、GPU、xPU作为硬件加速计算资源异构加速。
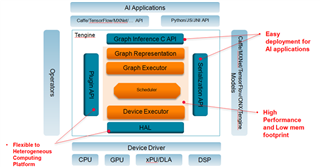
本文为Open AI Lab 工作人员投稿,对深度学习的核心操作GEMM进行了详细的使用介绍,欢迎对模型部署AI推断感兴趣的朋友关注。
很多刚入门的开发者想研读汇编代码,却苦于没有好的汇编入门教程,没有大神带入门汇编教程,自己看又看不懂,怎么办?福利来了,带来了一份超详细的gemm汇编教程。
GEMM简介
什么是GEMM?它的英文全称是 to (通用矩阵的矩阵乘法),Gemm在神经网络的计算中占据很重要的位置。Why gemm is at the heart of deep [1]介绍了为什么GEMM在深度学习计算中如此重要,以及卷积计算中是如何使用GEMM。
教程大纲
教程分为三部分:
Step1:纯C实现的gemm
Step2:调用的gemm
Step3: 中的gemm
运行这个教程的代码,你需要:
可以执行armv8汇编的环境,比如
linux操作系统:本教程的编译脚本使用的是
超简洁的教程源码

Step1: 纯C实现的gemm
step1部分的代码直接执行:
cd step1make./test
这个程序中我们计算的矩阵乘法是A(m,k) * B(k,n) =C(m,n):
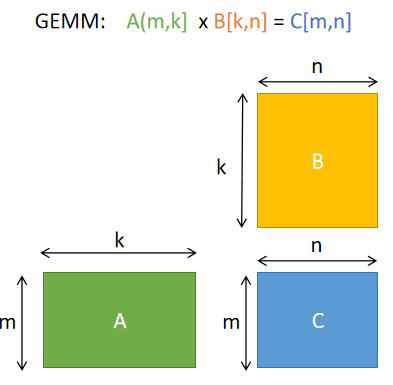
矩阵乘法的纯C简洁实现:
void gemm_pure_c(float* A, float* B, float* C,int m,int n,int k){for(int i=0;i<m;i++){for(int j=0;j<n;j++){C[i*n+j]=0.f;for(int p=0;p<k;p++){C[i*n+j]+=A[i*k+p]*B[p*n+j];}}}}
Step2: 调用的gemm
[2]是一个开源的基础线性代数计算库汇编教程,BLAS的英文全称Basic ,它在不同的处理器上都做了优化。在Linux上,可以直接通过apt-get安装这个库:
sudo apt-get install libopenblas-dev运行一下step2的代码
makeexport OMP_NUM_THREADS=1taskset 0x1 ./test
在上得到的结果是
[m n k]: 256 128 256[openblas]: 4.68 ms[pure c]: 32.22 ms[blas VS pure_C]: maxerr=0.000076
可以看出,调用库的性能明显优于纯C实现。
Step3:调用 16x4 的gemm
这部分教程以[3]源码中的e.S[4]为例子,对汇编代码做了一些简化,只支持k为4的倍数的情况。
在使用的4x16 之前,首先要对矩阵A和矩阵B的数据进行。什么是呢?叫交错排布,表示对数据进行重新排布,为了计算的时候读取数据时能更好地利用缓存。这里我们对矩阵A的数据是对m中的每16个元素进行重排,对矩阵B的数据是对n的每4个元素进行重排。
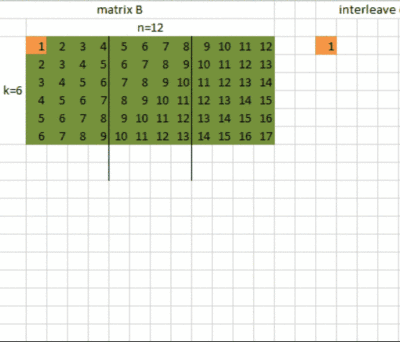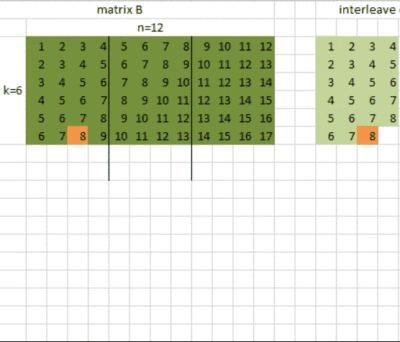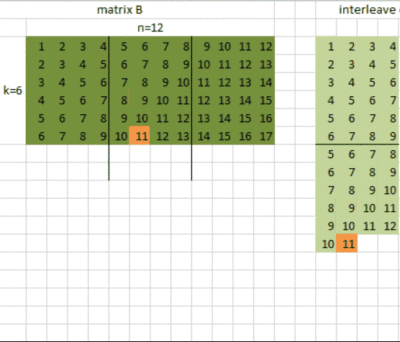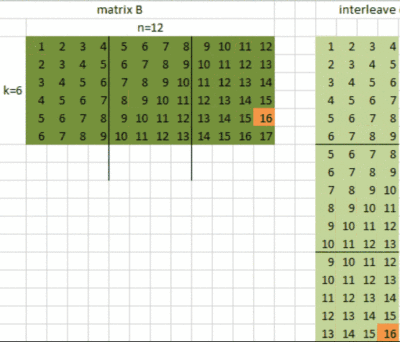
的4x16 计算的n=4,m=16的情况,目前支持的k是4的倍数:
我们在汇编代码的loop4中计算k的每四个元素.
ldr q0,[x1]ldr q1, [x1,0x10]ldp q2, q3, [x1,0x20]ldp q4, q5, [x2]ldp q6, q7, [x2,0x20]ldp q8, q9, [x2,0x40]ldp q10,q11,[x2,0x60]
下面的动图演示了4x16的的每条指令是如何进行计算的
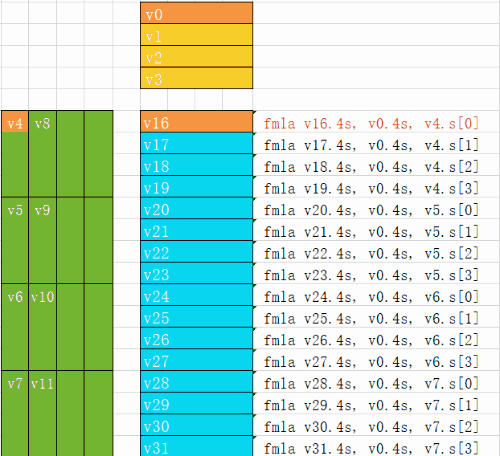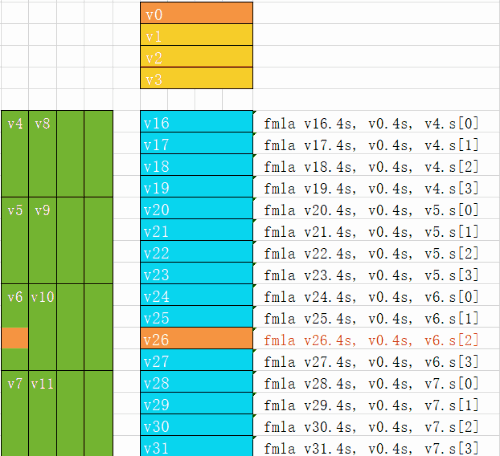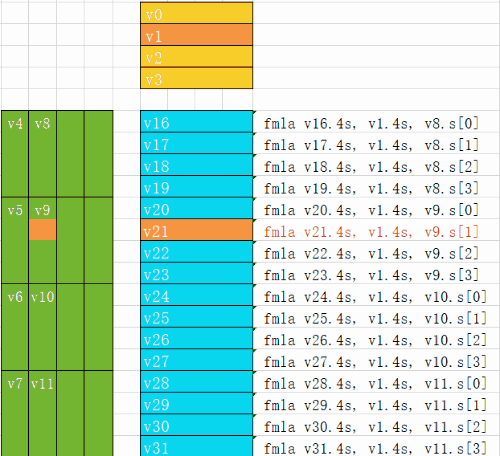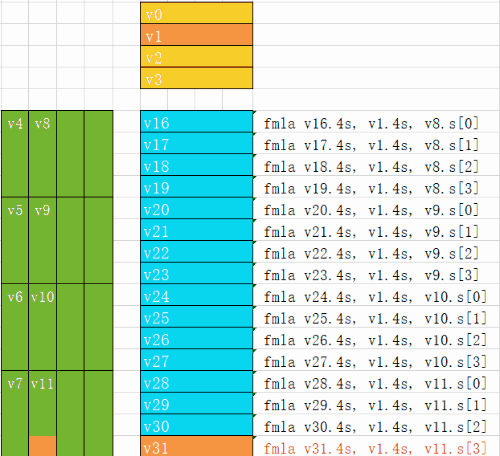
最后的汇编对应的是把输出数据保存
stp q16, q17 ,[x0]stp q18, q19 ,[x0, #0x20]stp q20, q21 ,[x0, #0x40]stp q22, q23 ,[x0, #0x60]stp q24, q25 ,[x0, #0x80]stp q26, q27 ,[x0, #0xa0]stp q28, q29 ,[x0, #0xc0]stp q30, q31 ,[x0, #0xe0]
我们在上执行step3的代码:
cd step3makeexport OMP_NUM_THREADS=1taskset 0x1 ./test
可以看出, 的4x16 性能在这三种实现中是最优的。
[m n k]: 256 256 256[tengine 4x16]: 7.71 ms[openblas]: 9.55 ms[pure c]: 316.00 ms[blas VS tengine]: maxerr=0.000061
What's more?
这个教程的代码只是一个示例,part3的代码只支持:
m是16的倍数
n是4的倍数
k是4的倍数
看完这个教程,建议可以尝试以下的一些拓展工作:
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh



