stats | 概率分布与随机数生成（二）——均匀分布、指数分布、正态分布、对数正态分布、卡方分布、t分布、F分布和增长分布

这是数学模型板块的第二篇推文，上篇介绍了几种离散型分布，从本篇开始介绍连续型概率分布。假定某个连续型分布的取值范围为[a, b]（a、b可以取无穷），则其概率密度函数与概率分布函数的关系：

x) = {int^b_{x}f(t)dt}" data--type="block-" style=" text-align: ; : auto; ">

1 均匀分布

如果在[a, b]范围内任意相同间隔长度内的概率是等同的指数分布，那么X就服从均匀分布（ ），记为。

均匀分布在取[a, b]间的任意值的概率密度函数都是。

stats中的相关函数有：

dunif(x, min = 0, max = 1, log = FALSE)
punif(q, min = 0, max = 1, lower.tail = TRUE, log.p = FALSE)
qunif(p, min = 0, max = 1, lower.tail = TRUE, log.p = FALSE)
runif(n, min = 0, max = 1)

# 概率密度
dunif(seq(1,11,0.5), 1, 11)

##  [1] 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1
## [20] 0.1 0.1

# 已知X求累积概率
punif(seq(1,11,0.5), 1, 11)

##  [1] 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 0.55 0.60 0.65 0.70
## [16] 0.75 0.80 0.85 0.90 0.95 1.00

# 已知累积概率求X
qunif(seq(0,1,0.05), 1, 11)

##  [1]  1.0  1.5  2.0  2.5  3.0  3.5  4.0  4.5  5.0  5.5  6.0  6.5  7.0  7.5  8.0
## [16]  8.5  9.0  9.5 10.0 10.5 11.0

# 生成符合均与分布的随机数
runif(10, 1, 11)

##  [1] 6.302010 5.699884 9.597925 9.065036 1.272223 7.165098 6.938233 3.395326
##  [9] 7.864294 5.044557

2 指数分布

在泊松过程中（事件在单位时间内发生次数的数学期望恒定，即），则事件第一次发生所需要的时间长度符合指数分布（ ），记为。

指数分布的概率密度函数：

0,\0 qquad x \end{array}right." data--type="block-" style=" text-align: ; : auto; ">

指数分布具有“无记忆性”，即

s)=P(x>T+s | t>T)" data--type="block-" style=" text-align: ; : auto; ">

stats中的相关函数有：

dexp(x, rate = 1, log = FALSE)
pexp(q, rate = 1, lower.tail = TRUE, log.p = FALSE)
qexp(p, rate = 1, lower.tail = TRUE, log.p = FALSE)
rexp(n, rate = 1)

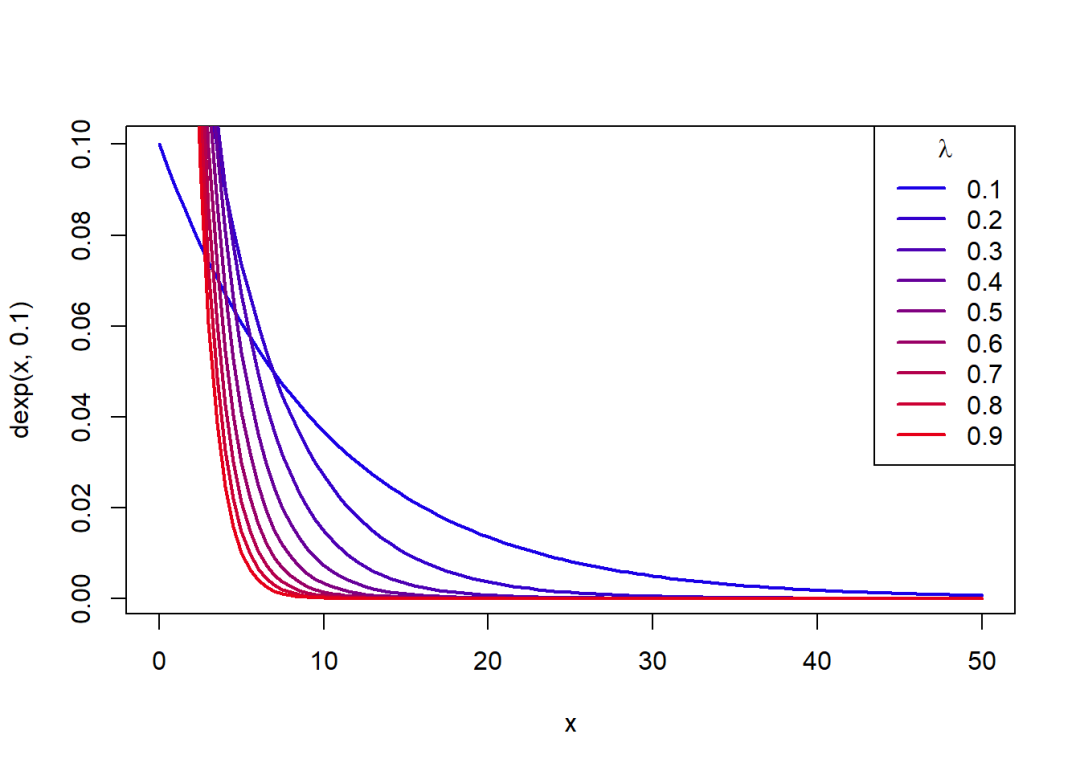
概率密度函数关于的变化图象：

curve(dexp(x, 0.1), 0, 50, col = rgb(0.1, 0, 0.9), lwd = 2)
for(i in seq(0.2, 0.9, 0.1)) {
  curve(dexp(x, i), 0, 50, col = rgb(i, 0, 1-i), lwd = 2, add = T)
}
legend("topright", legend = seq(0.1, 0.9, 0.1), lty = 1, xpd = T,
       col = c(rgb(seq(0.1, 0.9, 0.1), 0, 1-seq(0.1, 0.9, 0.1))),
       title = expression(lambda), lwd = 2)

3 正态分布

正态分布（ ），又称高斯分布（ ），记为。

正态分布的概率密度函数：

正态分布的性质：

stats中的相关函数有：

dnorm(x, mean = 0, sd = 1, log = FALSE)
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
rnorm(n, mean = 0, sd = 1)

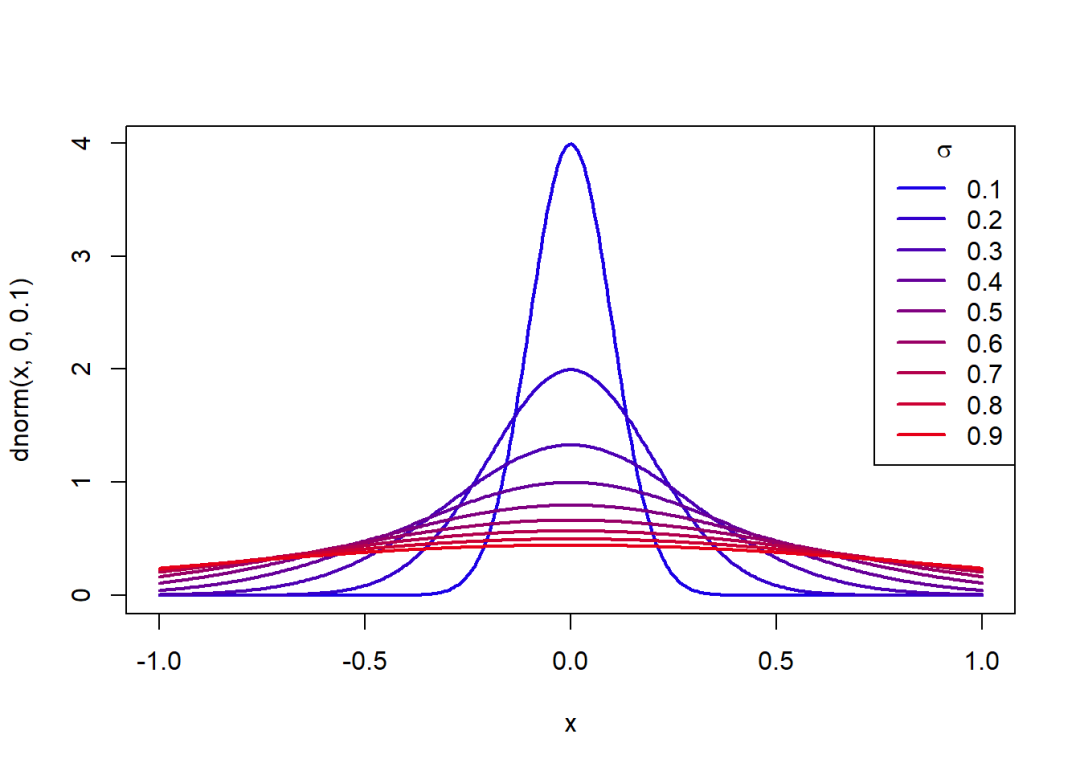
概率密度函数关于的变化图象：

curve(dnorm(x, 0, 0.1), -1, 1, col = rgb(0.1, 0, 0.9), 
      lwd = 2, n = 400)
for(i in seq(0.2, 0.9, 0.1)) {
  curve(dnorm(x, 0, i), -1, 1, col = rgb(i, 0, 1-i), 
        lwd = 2, add = T, n = 400)
}
legend("topright", legend = seq(0.1, 0.9, 0.1), lty = 1, xpd = T,
       col = c(rgb(seq(0.1, 0.9, 0.1), 0, 1-seq(0.1, 0.9, 0.1))),
       title = expression(sigma), lwd = 2)

4 对数正态分布

如果服从正态分布，则服从对数正态分布（Log ）。

对数正态分布的概率密度函数：

数学期望和方差：

stats中的相关函数有：

dlnorm(x, meanlog = 0, sdlog = 1, log = FALSE)
plnorm(q, meanlog = 0, sdlog = 1, lower.tail = TRUE, log.p = FALSE)
qlnorm(p, meanlog = 0, sdlog = 1, lower.tail = TRUE, log.p = FALSE)
rlnorm(n, meanlog = 0, sdlog = 1)

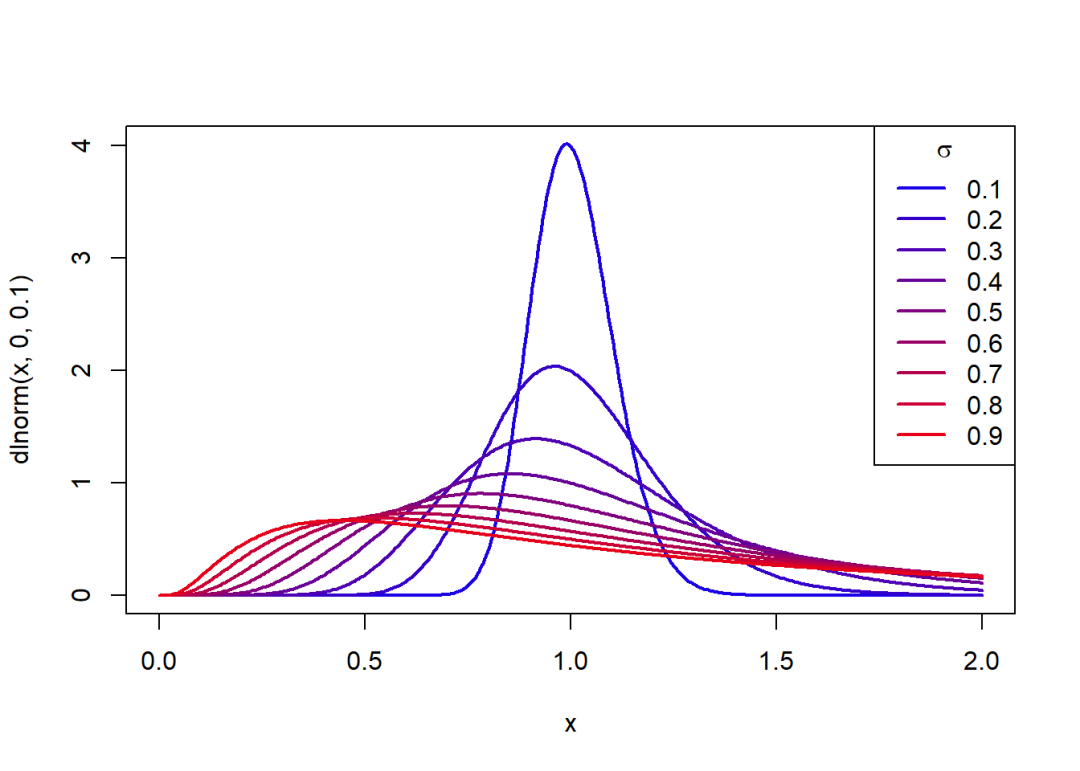
概率密度函数关于的变化图象：

curve(dlnorm(x, 0, 0.1), 0, 2, col = rgb(0.1, 0, 0.9), 
      lwd = 2, n = 400)
for(i in seq(0.2, 0.9, 0.1)) {
  curve(dlnorm(x, 0, i), 0, 2, col = rgb(i, 0, 1-i), 
        lwd = 2, add = T, n = 400)
}
legend("topright", legend = seq(0.1, 0.9, 0.1), lty = 1, xpd = T,
       col = c(rgb(seq(0.1, 0.9, 0.1), 0, 1-seq(0.1, 0.9, 0.1))),
       title = expression(sigma), lwd = 2)

5 卡方分布

n个互相独立且都服从标准正态分布的随机变量平方和服从卡方分布（Chi- ）,即

记为。称为卡方分布的自由度。

stats中的相关函数有：

dchisq(x, df, ncp = 0, log = FALSE)
pchisq(q, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)
qchisq(p, df, ncp = 0, lower.tail = TRUE, log.p = FALSE)
rchisq(n, df, ncp = 0)

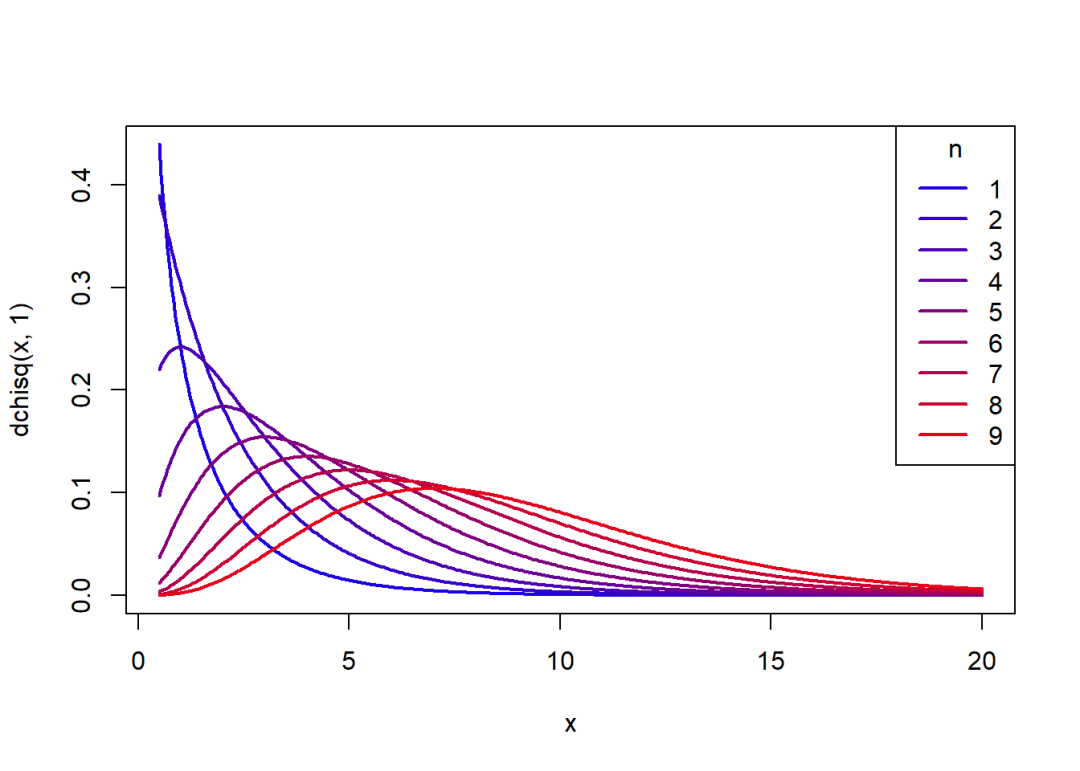
概率密度函数关于的变化图象：

curve(dchisq(x, 1), 0.5, 20, col = rgb(0.1, 0, 0.9), 
      lwd = 2, n = 400)
for(i in seq(0.2, 0.9, 0.1)) {
  j = 10*i
  curve(dchisq(x, j), 0.5, 20, col = rgb(i, 0, 1-i), 
        lwd = 2, add = T, n = 400)
}
legend("topright", legend = seq(1, 9, 1), lty = 1, xpd = T,
       col = c(rgb(seq(0.1, 0.9, 0.1), 0, 1-seq(0.1, 0.9, 0.1))),
       title = expression(n), lwd = 2)

6 t分布

若服从标准正态分布，服从自由度为的卡方分布，

则服从t分布（ t ）指数分布，记为。称为t分布的自由度。

t分布的自由度越大，越接近正态分布。

stats中的相关函数有：

dt(x, df, ncp, log = FALSE)
pt(q, df, ncp, lower.tail = TRUE, log.p = FALSE)
qt(p, df, ncp, lower.tail = TRUE, log.p = FALSE)
rt(n, df, ncp)

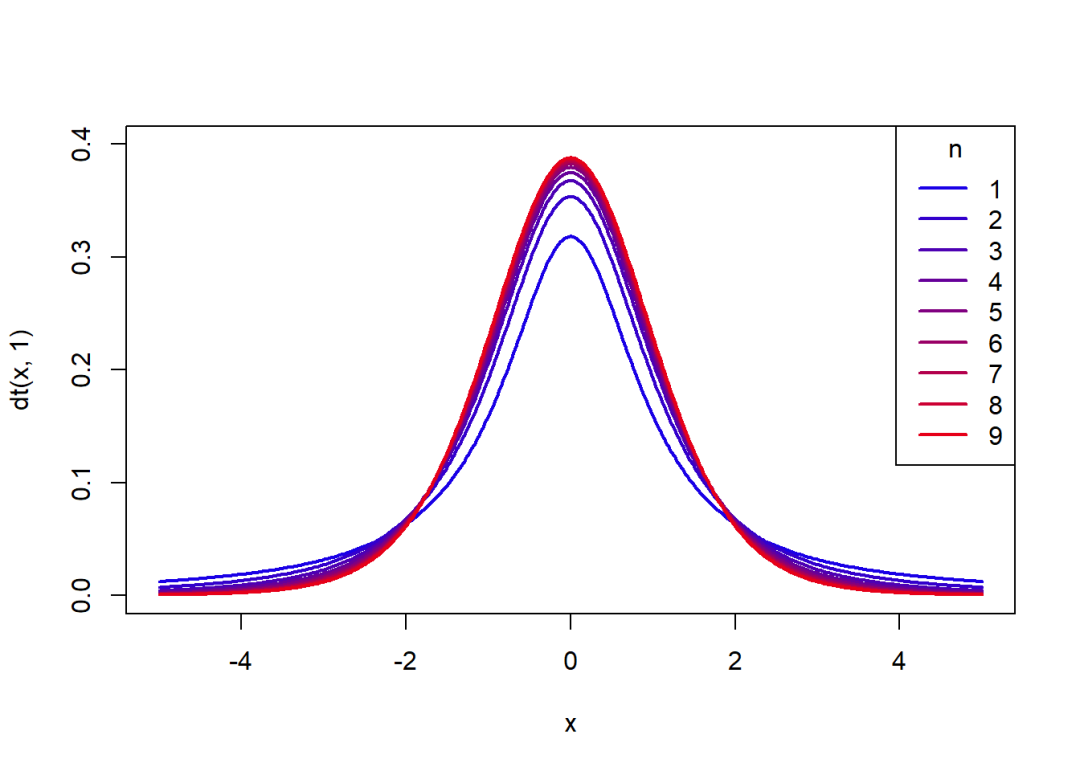
概率密度函数关于的变化图象：

curve(dt(x, 1), -5, 5, col = rgb(0.1, 0, 0.9), 
      lwd = 2, n = 400, ylim = c(0, 0.4))
for(i in seq(0.2, 0.9, 0.1)) {
  j = 10*i
  curve(dt(x, j), -5, 5, col = rgb(i, 0, 1-i), 
        lwd = 2, add = T, n = 400)
}
legend("topright", legend = seq(1, 9, 1), lty = 1, xpd = T,
       col = c(rgb(seq(0.1, 0.9, 0.1), 0, 1-seq(0.1, 0.9, 0.1))),
       title = expression(n), lwd = 2)

7 F分布

若和分别服从自由度为和的卡方分布，

则服从F分布（F ），记为。和称为F分布的自由度。

stats中的相关函数有：

df(x, df1, df2, ncp, log = FALSE)
pf(q, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)
qf(p, df1, df2, ncp, lower.tail = TRUE, log.p = FALSE)
rf(n, df1, df2, ncp)

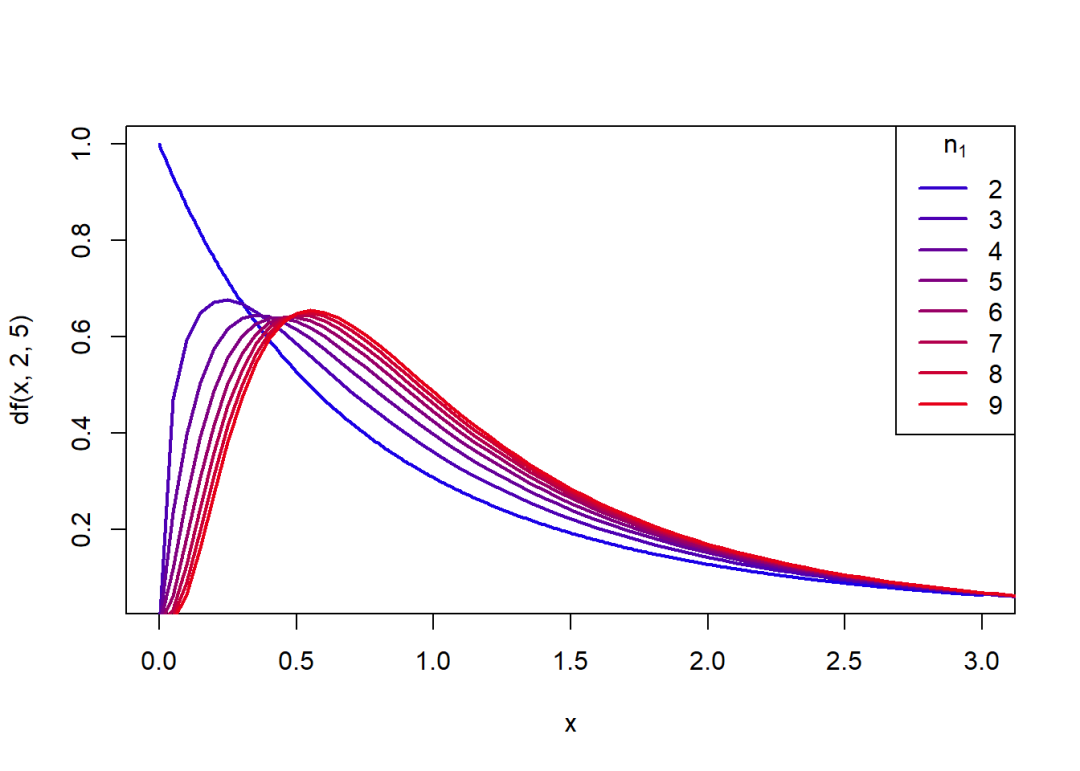
概率密度函数关于的变化图象：

curve(df(x, 2, 5), 0, 3, col = rgb(0.1, 0, 0.9), 
      lwd = 2, n = 400)
for(i in seq(0.3, 0.9, 0.1)) {
  j = 10*i
  curve(df(x, j, 5), 0, 20, col = rgb(i, 0, 1-i), 
        lwd = 2, add = T, n = 400)
}
legend("topright", legend = seq(2, 9, 1), lty = 1, xpd = T,
       col = c(rgb(seq(0.2, 0.9, 0.1), 0, 1-seq(0.2, 0.9, 0.1))),
       title = expression(n[1]), lwd = 2)

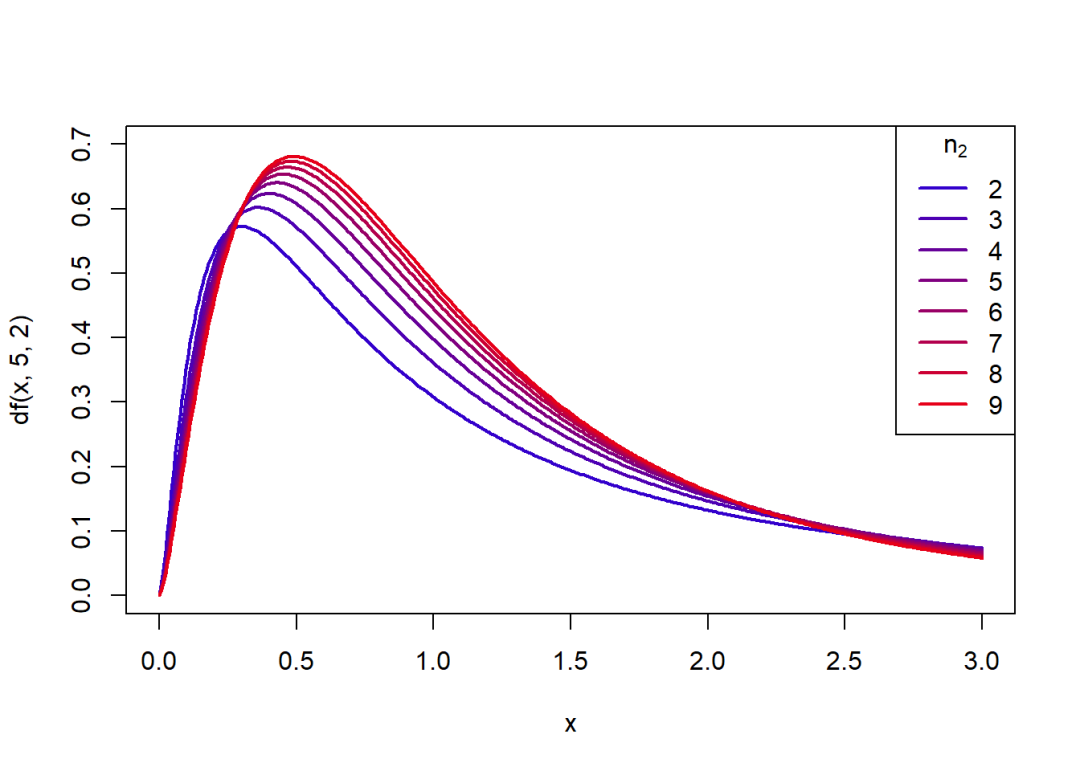
概率密度函数关于的变化图象：

curve(df(x, 5, 2), 0, 3, col = rgb(0.1, 0, 0.9), 
      lwd = 2, n = 400, ylim = c(0, 0.7))
for(i in seq(0.2, 0.9, 0.1)) {
  j = 10*i
  curve(df(x, 5, j), 0, 3, col = rgb(i, 0, 1-i), 
        lwd = 2, add = T, n = 400)
}
legend("topright", legend = seq(2, 9, 1), lty = 1, xpd = T,
       col = c(rgb(seq(0.2, 0.9, 0.1), 0, 1-seq(0.2, 0.9, 0.1))),
       title = expression(n[2]), lwd = 2)

8 分布

逻辑斯蒂分布（ ）,又称增长分布。其

概率分布函数:

概率密度函数：

stats中的相关函数有：

dlogis(x, location = 0, scale = 1, log = FALSE)
plogis(q, location = 0, scale = 1, lower.tail = TRUE, log.p = FALSE)
qlogis(p, location = 0, scale = 1, lower.tail = TRUE, log.p = FALSE)
rlogis(n, location = 0, scale = 1)

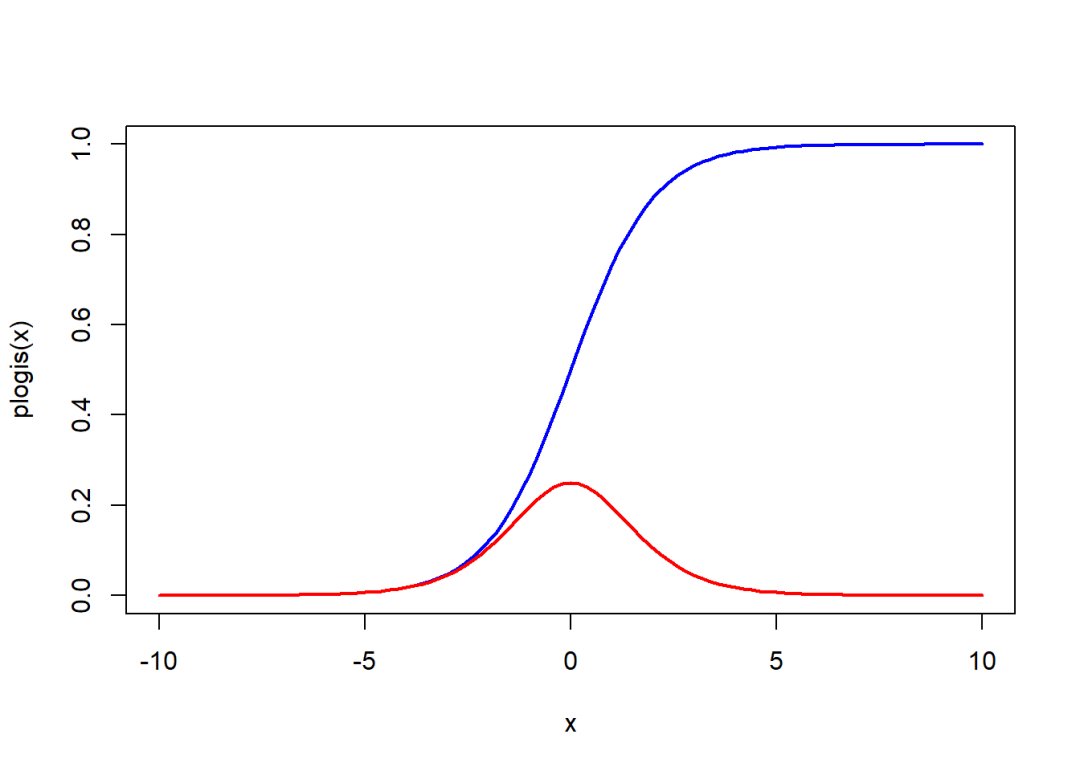
标准分布的累积概率函数和概率密度函数：

curve(plogis, -10, 10, col = "blue", lwd = 2)
curve(dlogis, -10, 10, col = "red", lwd = 2, add = T)

限时特惠:本站持续每日更新海量各大内部创业课程，一年会员仅需要98元，全站资源免费下载
点击查看详情

站长微信:Jiucxh