千 言 万 语 不 及 一 张 图。
——佚名
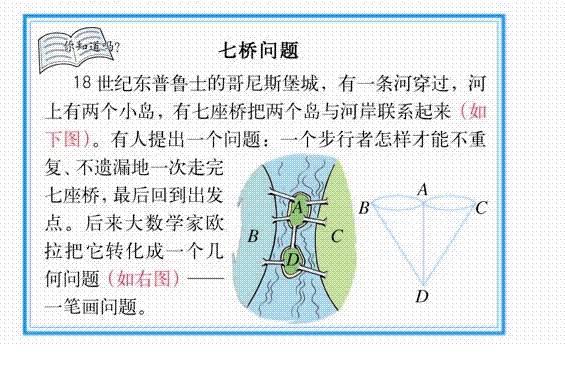
上面介绍的就是著名的哥尼斯堡七桥问题(The Seven )。如果你感兴趣可以先在图上“纸上漫步”,看看能不能找出一条符合要求的路线来。当然,在进行了无数次试验后你会发现找不到符合要求的路线,你也许会猜测这样的路线根本不存在!当年住在哥尼斯堡的人们也是这样猜测的,但却不能说明为什么。这个问题难坏了哥尼斯堡人,直到1727年昂那德克·欧拉( Euler, 1707~1783年)的出现。

欧拉,瑞士人,在他20岁的时候,被俄国请去在圣彼得堡(原列宁格勒)的科学院做研究。在圣彼得堡工作期间,欧拉从他的朋友那里得知了“七桥问题”,欧拉也相信这一结论是正确的,但是欧拉并不像普通人那样,去当地实际行走来证明这个结论。作为一个数学工作者,他把“七桥问题”的地图,抽象为一个平面图形。他用点A、B、C、D分别代表4块陆地,点之间用线相连,两点之间是否连线,并且连几条线,取决于这两个点所对应的陆地之间有几座桥。这样7条线就代表了7座桥,如下图。
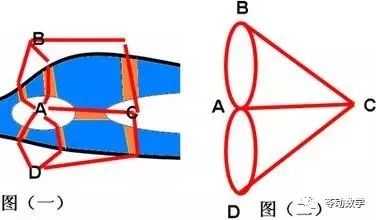
我们称,从图上任意一点出发,经过图中每条线一次且仅一次,再回到原来的出发点的路线为欧拉回路。于是,七桥问题就变成了右图中是否存在欧拉回路的问题。欧拉证明这个回路是不存在的。欧拉高明之处更在于他讨论了一般的图是否存在欧拉回路的本质特征,而且还圆满地给出了这个特征。除了欧拉回路,还有欧拉半回路。欧拉半回路是指经过图中每条线一次且仅一次,不要求一定回到出发点的路。容易看出,欧拉回路是欧拉半回路的特例。从一个点出发的线的条数被称为这个点的度数。度数为偶数的点叫做偶点;度数为奇数的点叫做奇点。
欧拉的成就体现在下述命题七桥问题,后人称为欧拉定理:
在一个连通的图中七桥问题,
(1)如果奇点的个数大于2,那么不存在欧拉回路和欧拉半回路;
(2)如果奇点的个数等于2,那么它不存在欧拉回路,但存在欧拉半回路。这个半回路,一定是从这两个奇点之一出发,最后到达另一个奇点;
(3)如果奇点的个数为0,则存在欧拉回路,而且可以从任意一点出发得到它(当然,起点即为终点)。
这是一个具有拓扑意义的结论,这个结论刊登在1736年欧拉发表的论文《哥尼斯堡七桥问题》中,从此人们称欧拉为数学的一个分支——图论(低维拓扑)的鼻祖。
如今哥尼斯堡的七座桥只剩下三座,一条新的跨河大桥已经建成,它完全跨过河心岛——内福夫岛。
虽然七桥问题已成为历史,但是遗留下来的卓越的解答和数学方法将永载史册。
实际上,图的欧拉半回路问题就是图的一笔画问题。如果一个图不能一笔画出,也就是没有欧拉半回路,那么至少需要几笔才能画出?对于这个问题,早已经有了圆满的回答。首先应该知道,任何图的奇点的个数一定是偶数(原因是:一条线产生2度)。这个偶数的一半,就是这个图可以画出的最少笔数。这个问题的另一个提法是:如果一个图不是一笔画,那么在这个图上至少加几条线,能够使它成为一笔画?容易看出,答案是上面提到的最少笔数减一。还可以提出进一步的问题:如果认为图中的线有长度,怎样加线,能够使所加线的总长度最小而同时保证它是一笔画?这个问题的实际模型,正是我国著名数学家管梅谷先生在1962年提出的“中国邮递员问题”(The )。
今天,图论已广泛应用在计算机科学、运筹学、控制论、信息论等学科中,成为对现实世界进行抽象的一个强有力的数学工具。
数学问题的提出与解决,推动了数学的发展。我们今天学习欧拉的成果不应是单纯把它作为数学游戏看待,重要的是应该知道他是怎样把一个实际问题抽象为数学模型,然后用数学的方法研究它,再用来解决实际问题。这样循环往复,螺旋上升,永无止境。欧拉的大作就是我们学习的一个样板。
让数学
动
起来
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh