是一个由谷歌公司开发的人工智能程序,它在围棋等棋类游戏中取得了惊人的胜利。这个程序的核心算法是蒙特卡洛树搜索(Monte Carlo Tree , MCTS),它是一种基于随机模拟的搜索算法,可以在很短的时间内找到最优的决策。
蒙特卡洛树搜索算法的基本思想是通过随机模拟对可能的决策进行评估,然后选择最优的决策。具体来说,该算法的过程分为四个步骤:选择、扩展、模拟和反向传播。
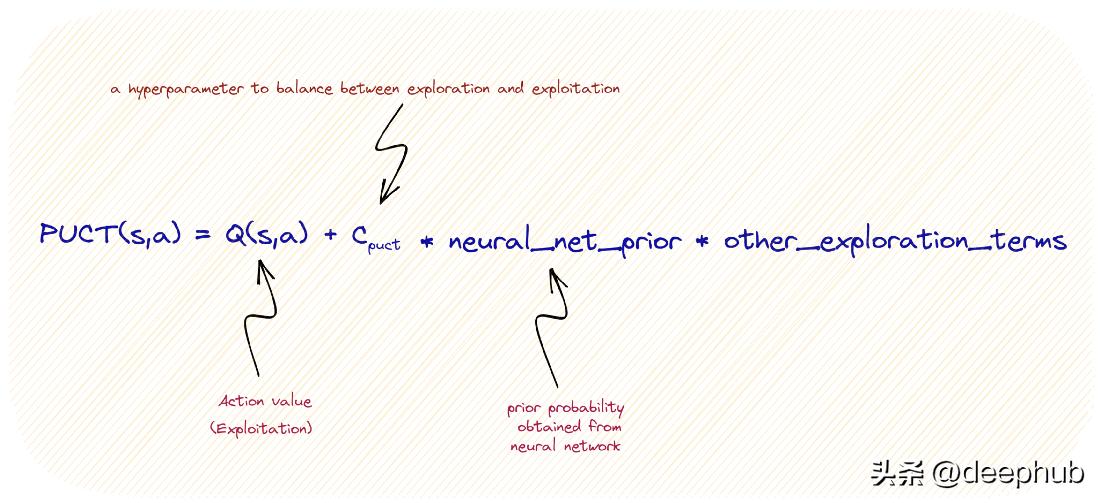
1选择():从根节点开始,按照一定策略选择一个节点进行扩展。通常使用Upper Bound 1 to trees(UCT)算法来确定每个节点的选择概率。UCT算法将选择概率分为两部分:一部分是节点的平均值,另一部分是节点的探索程度(即节点的访问次数)的倒数的平方根,两部分加权求和即为节点的选择概率。
2扩展():对选定的节点进行扩展,即生成其所有可能的子节点。
3模拟():对于扩展生成的子节点,使用随机策略进行模拟,直到达到某个终止条件,例如游戏结束或达到最大模拟次数。
4反向传播():根据模拟结果,更新每个节点的统计信息,例如节点的访问次数和累计收益。这些统计信息将被用于计算每个节点的价值估计,从而影响下一次选择。
蒙特卡洛树搜索算法的优点在于它可以在不完全信息和高复杂度的环境中找到最优解,且不需要预先学习策略或价值函数。在中,该算法被用于选择最优的下棋位置。具体来说,使用了两个神经网络:一个用于策略估计,另一个用于价值估计。在选择节点时,使用策略网络来评估每个可能的下棋位置,然后使用蒙特卡洛树搜索算法来选择最优的位置。在模拟阶段,使用价值网络来评估模拟结果,从而更新每个节点的统计信息。通过不断迭代,可以得到一个越来越准确的价值估计和策略估计,从而下出更优秀的棋局。
蒙特卡洛树搜索算法的另一个优点在于它可以通过多线程并行化来加速计算。在中,该算法被并行化到数千个CPU和GPU上蒙特卡洛树搜索,以实现高效的计算。此外,还使用了一些优化技巧,例如Move (MAS)和 (PD),进一步提高了算法的效率和准确性。

总之,蒙特卡洛树搜索算法是背后的核心算法,它通过随机模拟和反向传播来寻找最优解决策,具有在不完全信息和高复杂度环境中找到最优解的优点。在中,该算法被用于选择最优的下棋位置蒙特卡洛树搜索,结合神经网络的策略估计和价值估计,实现了高效的计算和准确的棋局判断。蒙特卡洛树搜索算法不仅在围棋等棋类游戏中取得了成功,在其他领域,如路径规划、机器人控制、自动化决策等方面也有广泛应用和研究。
如果有任何疑问可以随时评论留言或私信我,欢迎关注我[点击关注],共同探讨。
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh