需要观看本讲座完整视频的,请扫描下方二维码,登录微师平台观看。
作业点评
利用上节课讲解的内容,掌握数学原理,根据规律作图。


典例分析
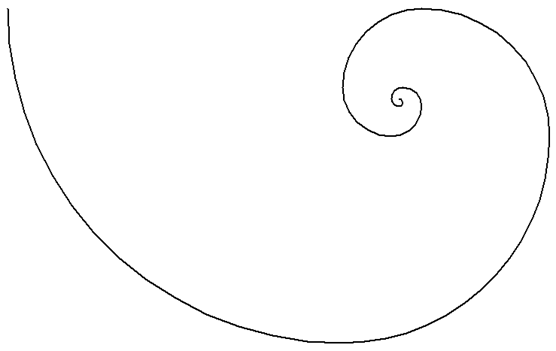
斐波那契螺旋线也称"黄金螺旋",是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案。
斐波那契数列第1项和第2项都是1,从第3项开始,每一项都等于前两项之和,即1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233海龟作图,……
"""
on Mon Jul 20 22:40:59 2020
@: 巧若拙
斐波那契螺旋线也称"黄金螺旋",是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案。
"""
as tt
tt.. = True # 启动绘图,在IDE中运行加这句可避免报错
tt.(2)
tt.speed(3)
rs = [1, 1]
for i in range(2, 11):
rs.(rs[-2] + rs[-1])
for r in rs:
tt.(-r*5, 90)
tt.ht()#隐藏笔头
tt.done()
"""
on Sun Jul 19 10:51:37 2020
@: 巧若拙
斐波那契螺旋线也称"黄金螺旋",是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案。
"""
as tt
#绘制正方形及1/4圆弧
def (r):
#顺时针画蓝色正方形
tt.color("blue")
for i in range(4):
tt.(r)
tt.right(90)
#顺时针画红色1/4圆弧
tt.color("red")
tt.(-r, 90)
tt.. = True # 启动绘图,在IDE中运行加这句可避免报错
tt.(2)
tt.speed(3)
rs = [1, 1]
for i in range(2, 11):
rs.(rs[-2] + rs[-1])
for r in rs:
(r*5)
tt.ht()#隐藏笔头
tt.done()
拓展思考
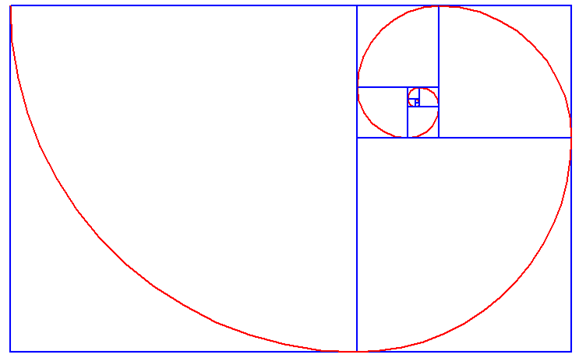
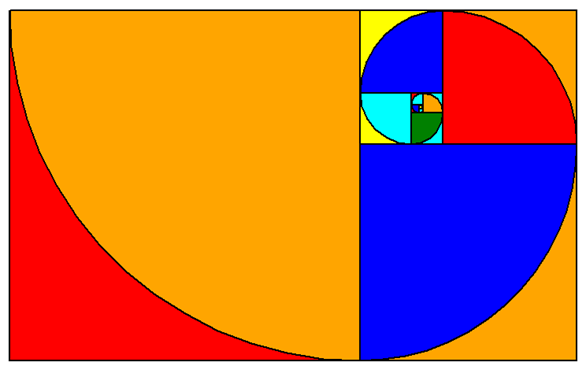
除了单纯地绘制斐波那契螺旋线,我们还可以添加正方形和填充背景颜色来突出螺旋线。
"""
on Mon Jul 20 22:56:54 2020
@: 巧若拙
斐波那契螺旋线也称"黄金螺旋"海龟作图,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案。
"""
as tt
#绘制正方形及1/4圆弧
def (r, ):
tt.color("black", [0])
tt.()
#顺时针画1/2正方形
for i in range(2):
tt.(r)
tt.right(90)
tt.()
#顺时针画剩余1/2正方形及1/4圆弧
tt.color("black", [1])
tt.()
for i in range(2):
tt.(r)
tt.right(90)
tt.(-r, 90)
tt.()
tt.. = True # 启动绘图,在IDE中运行加这句可避免报错
tt.(2)
tt.speed(2)
= ('red','','','green','cyan','blue')
rs = [1, 1]
for i in range(2, 11):
rs.(rs[-2] + rs[-1])
for r in rs:
c = .(, 2) #随机获取2种颜色
(r*5, c)
tt.ht()#隐藏笔头
tt.done()
课后练习
请使用海龟绘图画出如下图形:
1.等大的圆点构成一个圆

2.直径递增的圆点构成递增圆弧

3.每5个圆点一组,直径按斐波那契数列递增,构成斐波那契螺旋线。

参考答案
如果你有好的答案,可以留言或私信斌哥,有机会在下节课程的‘’作业点评‘’环节出镜哦!
需要本文word版的,可以加入“算法之旅”知识星球参与讨论和下载文件,“算法之旅”知识星球汇集了数量众多的同好,更多有趣的话题在这里讨论,更多有用的资料在这里分享。
我们专注算法,感兴趣就一起来!
相关优秀文章:
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh




