【学习导引】本期课我们来学习排列组合与二项式定理。
一、分类加法计数原理
1.分类加法计数原理
完成一件事有两类不同的方法,在第类方案中有种不同的方法,在第类方案中有种不同的方法,那么完成这件事共有种不同的方法.
2.分类加法计数原理的推广
完成一件事有类不同的方法,在第类方案中有,种不同的方法,在第类方案中有种不同的方法,……,在第类方案中有种不同的方法排列组合二项式定理,那么完成这件事共有种不同的方法.
3.分类加法计数原理的特点
分类加法计数原理可简称为分类计数原理或加法原理,其特点是各类中的每一个方法都可以完成要做的事情.
二、分步乘法计数原理
1.分步乘法计数原理
完成一件事需要两个步骤,做第步有种不同的方法,做第步有种不同的方法,那么完成这件事共有种不同的方法.
2.分步乘法计数原理的推广
完成一件事有个步骤,做第步有种不同的方法,做第步有种不同的方法,…….,做第步有种不同的方法,那么完成这件事共有种不同的方法.
3.分步乘法计数原理的特点
分步乘法计数原理可简称为分步计数原理或乘法原理,其特点是每一步都要使用一种方法才能完成该步要做的事情.可以用下图表示分步乘法计数原理,图中的箭头强调要依次完成各步骤才能完成要做的事情.
三、排列
1.排列的概念
一般地,从个不同元素中取出个元素,按照一定的顺序排成一列,叫做从个不同元素中取出个元素的一个排列.如果,一般称为选排列;如果,则称为全排列.
两个排列相同的含义:两个排列的元素完全相同,并且元素的排列顺序也相同。
2.排列数与排列数公式
①排列数的定义:从个不同元素中取出个元素的所有不同排列的个数叫做从个不同元素中取出个元素的排列数,用符号表示.
②排列数公式
这里,且,这个公式叫做排列数公式.
3.全排列、阶乘与排列数公式的阶乘表示
①全排列: 个不同元素全部取出的一个排列,叫做个元素的一个全排列.这时公式中,即有.
②阶乘:个不同元素全部取出的排列数,等于正整数到的连乘积.正整数到的连乘积,叫做的阶乘,用表示,所以个不同元素的全排列数公式可以写成.规定,这是一种规定,不能按阶乘的含义解释.
③排列数公式的阶乘表示
因为
所以排列数公式还可以写成:
四、组合
1.组合的概念
一般地,从个不同元素中取出个元素合成一组排列组合二项式定理,叫做从个不同元素中取出个元素的一个组合.
【对组合的理解】
(1)给出的个元素必须互不相同.
(2)抽取的个元素是从个不同的元素中不重复地抽取的,因而这个元素也是互不相同的,即在这里既没有重复的元素,也没有重复抽取同一元素的情况.
(3)组合的定义中包含两个基本内容:一是“取出元素”,二是“合成一组”,“合成一组”就是与顺序无关,无序性是组合的本质.
(4)根据组合的定义,只要两个组合中的元素完全相同,那么不管元素的顺序如何,都是相同的组合,只有当两个组合中的元素不完全相同时,才是不同的组合.
2.组合数与组合数公式
①组合数
从个不同元素中取出个元素的所有不同组合的个数,叫做个不同元素中取出个元素的组合数,用符号表示.
②组合数公式
连乘表示式:,且)
阶乘表示式:,且)
③在公式中,我们规定,因而有,同样.
五、二项式定理
1.二项式定理
一般地,对于任意正整数,都有
这个公式叫作二项式定理.等号右边的多项式叫作的二项展开式,其中各项的系数叫作二项式系数.
二项展开式的第项叫作二项展开式的通项.它体现了二项展开式的项数、系数、次数的变化规律,是二项式定理的核心,它在求二项展开式的某些特定的项及其系数方面有着广泛的应用.
2.二项式定理的性质
一般地,展开式的二项式系数有如下性质:
①对称性:.
②
③增减性与最大值:
当时, ;当 \frac{n-1}{2}" data--type="-" style="">时, C_n^{r+1}" data--type="-" style=""> ;故当为偶数时,二项式系数中,以最大;
当为奇数时,二项式系数中,以和(两者相等)最大;
④各二项式系数的和:.
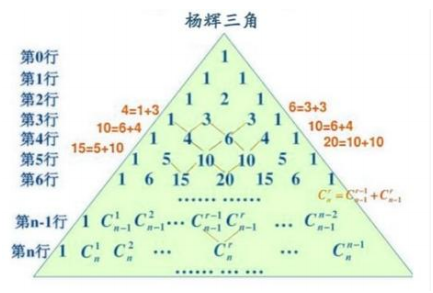
以上各性质均可由杨辉三角作对比.
公众号菜单让您方便查阅历史文章
传播知识 惠及大众
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh