前言
盾构机时间序列数据的分割是基于对数据的特征提取和模式识别,旨在将连续记录的数据划分为不同的状态区间,以便进行进一步的分析和预测。
传统的线性方法在面对复杂的非线性问题时效果有限,因此需要探索更准确的非线性自回归方法。
以多元非线性自回归模型进行拟合,用最小二乘法拟合参数。
通过拟合出的模型得到各个时间段的误差,再利用误差进行动态规划,最后对实际数据进行分割试验。

多元非线性自回归理论公式
1.1非线性自回归模型构造原理
常见的ARMA(n,m)模型为:
式中:ωt———观测值;φi,θj———不同量的参数;xt-i———观测值的列向量;at———白噪声。
根据函数逼近理论中的Weierstrass定理,任何定义于一个闭区间的连续函数可以用多项式任意准确地逼近。
因此,非线性函数可以在一个闭区间内近似地采用多项式逼近,其表达式可以写为:
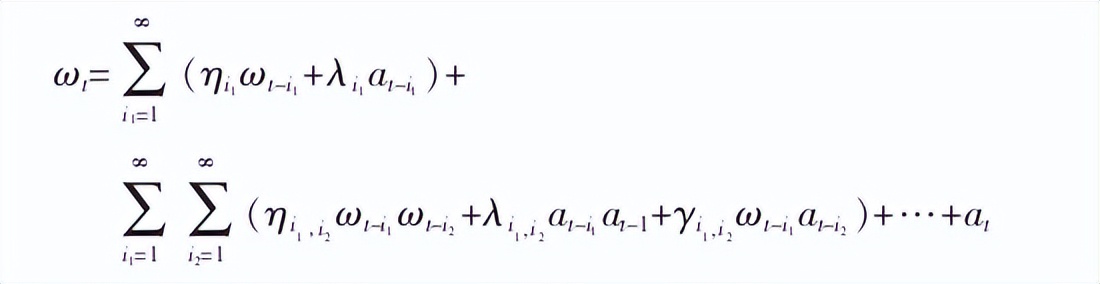
式中:λi1,ηi1,i2,λi1,i2,γi1,i2———模型参数。
上式描述的系统具有零初始状态(即ω0=ω-1=ω-2=…=0),且系统在初始时刻t=0之前无输入,则有:ω2=a1,通过不断地反代入最终能得到:
式中:αi1,αi1,i2,…———模型参数;p———多项式展开的阶次;nj(j=1,2最小二乘法,…,p)———各子项的记忆步长。
上式描述的模型称为非线性自回归时间序列一般表达式模型,简记为GNAR(p;n_1,n_2,,n_p)模型。
1.2 非线性自回归模型的参数估计
最小二乘法估计不需要样本数据提供概率统计方面的信息,并且统计结果有很好的统计特性,令:
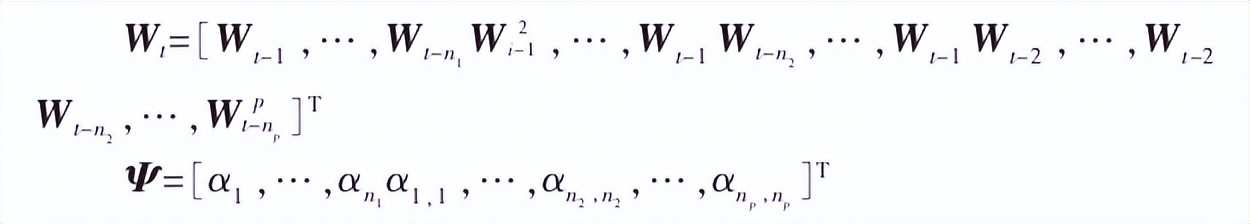
则得到:
于是,参数Ψ的最小二乘估计为:
式中:
Y=[wt,wt+1,…,wt+k]T
W=[Wt,Wt+1,…,Wt+k]T
1.3 向量自回归模型
随机过程可描述为:
上式称为p阶向量自回归模型,记为VAR(p),其中yt=(y1t,y2t,…,ykt)T是K维随机向量,Ai是K×K维自回归系数矩阵。
v是K维截断项,ut=(u1t,u2t,…,ukt)T是K维白噪声,满足VAR(p)模型的过程称为VAR(p)过程。
通过向量表示,K维VAR(p)模型可转化为Kp维VAR(1)模型:

用最小二乘法估计回归参数,则离差平方和方程为:
在求A的时候,必须要求(yT-y)-1存在,则yT-y必须是一个非奇异矩阵,由线性代数的知识可知,yT-y为p+1阶满秩矩阵,则:
n≥p+1
说明在回归计算之前必定要满足样本数量大于回归数,多项式自回归是一种可以转化为线性自回归的一种重要模型,m阶多项式回归模型:
当多项式回归的阶数不一样的时候,回归出来的曲线有很大的区别
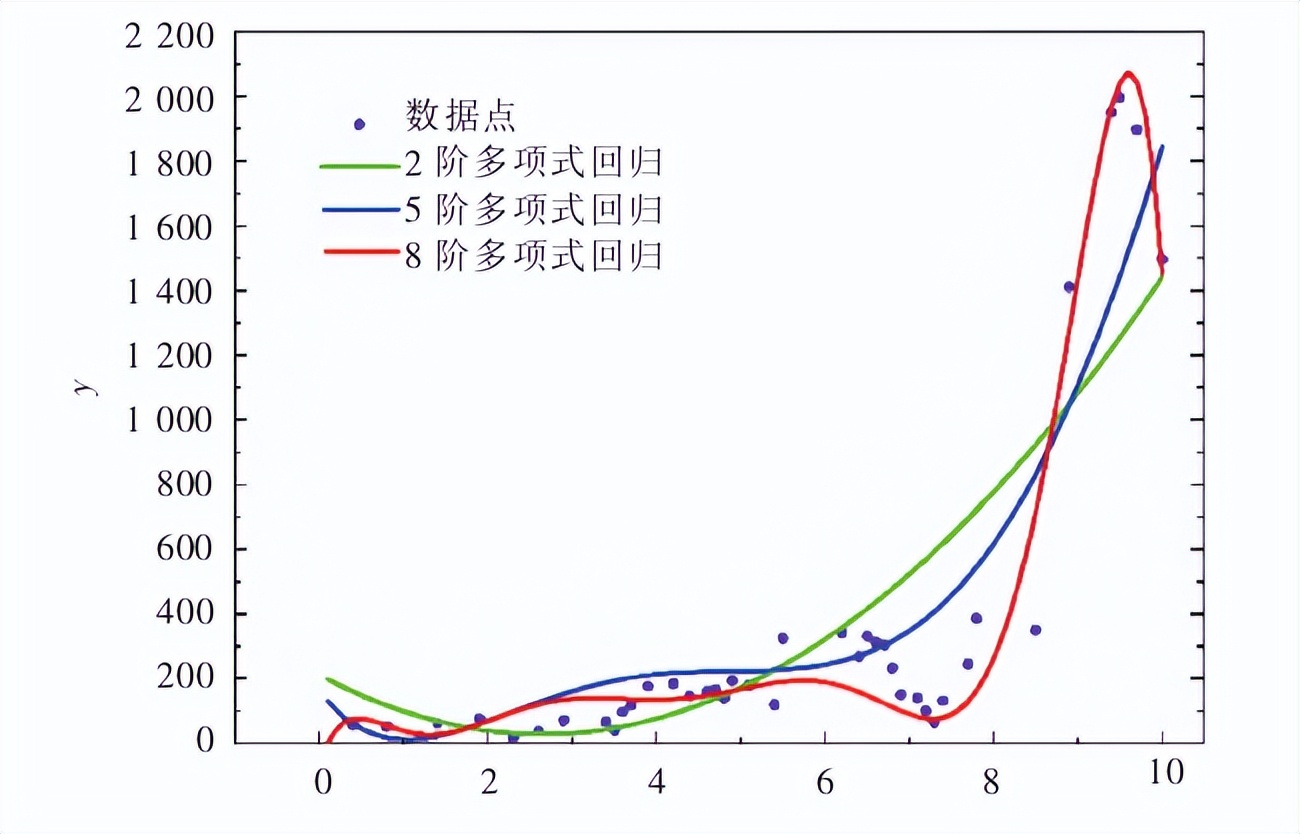
同时还存在多元多阶多项式回归模型:
如上式所示,式中最高次数一定是大于1的,显然是个非线性回归模型。
但是如果把式中次数大于1的自变量用另一个一次自变量代替时,非线性回归模型转化为线性回归模型:

动态规划算法推导
假设分割出的每一段必须包含两段数据,其中E(i,j)表示第i到第j段的真实误差,Ca(I,J)表示第I到J段划分为a段时的最小误差,YK表示进行不同段的数据,所以动态规划的步骤如下:
第1步:通过上一节所说的算法得到的不同数据段的误差就是E(i,j),与之联系的几个YK则表示的是这个误差来源,得到E(i,j)表示第i到第j段时间中通过非线性自回归拟合得到数据与真实数据的误差值。
第2步:通过比较得到不同时间段分割两段时的最优误差值(这是可以直接通过比较得到的)。
如下图上半部分将5个数据分两段进行比较,其他不管多大的数据量分割两段也能以此类推。
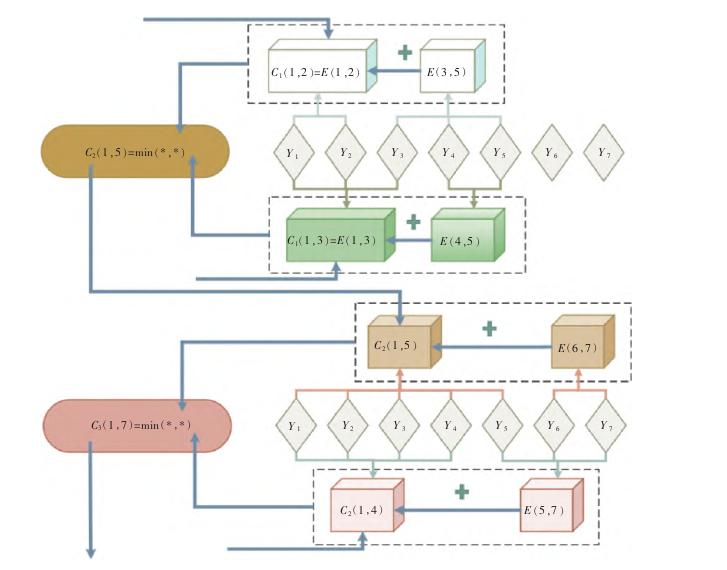
第3步:接下来是分割3段,分割3段需要用到分割两段的结果,上半部分5个数据只能分两段,于是通过比较得到C2(1,5)前5个数据分两段的最优情况。
得到最优后通过下面半个部分可以看到7个数据进行3段分割有两种情况:C2(1,5)+E(6,7)和C2(1,4)+E(5,7)。
其中C2(1,5)是5个数据的局部最优误差,最终通过比较就能得到分3段的最优解,同样的对于更多的数据量也是用这一样的方法进行3段的分割。
第4步:进行4段的分割,也就是用3段分割的最优解误差加上一段的误差进行比较得到4段分割的最优解,于是不论多少段的分割都能够进行分割了。
通过不断地相加比较等步骤能得到:
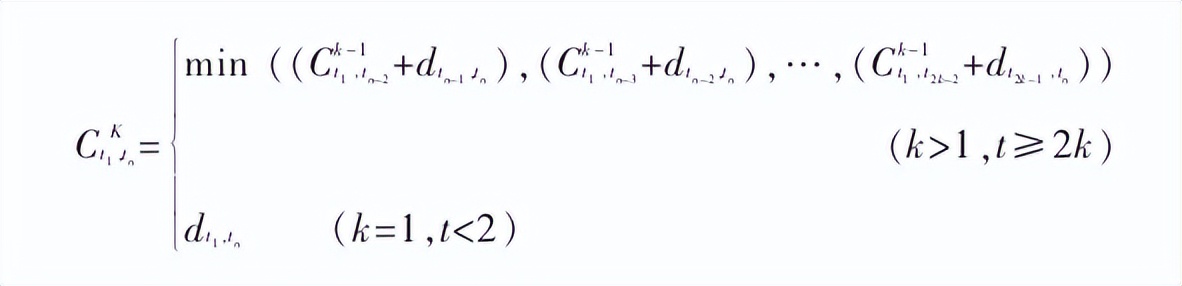
式中:dti,tj———时刻ti到时刻tj之间样本数据的误差值;Ck-1t1,tn-2———比较之后得到的最优解误差。

盾构机时间序列分割
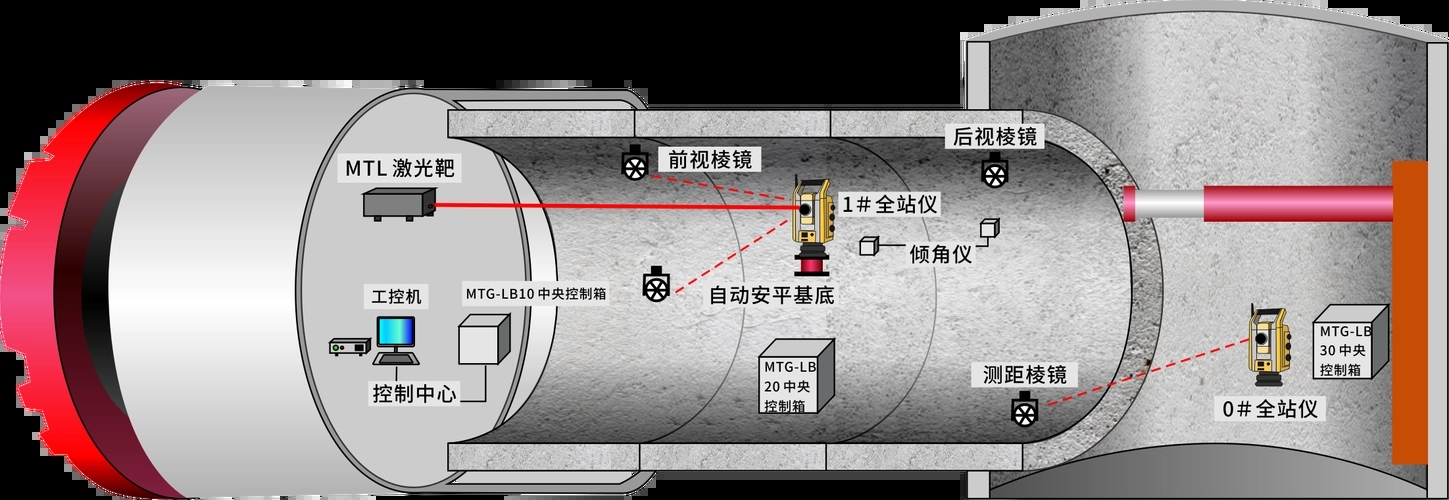
我国某城市地铁隧道掘进工程隧道的全长为2000m,剖面直径为6.4m,掘进中采用土压平衡盾构机(EPB)。
这款盾构机包括刀头、箱体、机尾外壳、螺旋输送机等辅助子系统,盾构机的直径为6.2m,质量超过500t。
在它刀头的刀库里一共含有120把刀具,后面采用的数据分别来自盾构机掘进过程中的3种施工状态,所以将目标数据分为3类。
但由于盾构机体积过于庞大,结构复杂,外加只能使用笔记本电脑进行计算,所以只取一些相关的数据进行分析。
3.1设计试验
刀盘转矩T是盾构机运行参数中最重要的参数之一,并且刀盘转矩T能够反应盾构机状态,所以将T作为主要分割对象,结合膨润土压力、螺机转矩。

A组推进位移进行一次综合的时序分割计算,在得到的数据中,3种工况下,分别取刀盘转矩T,螺机转矩,A组推进位移对应的400个样本作为试验数据集。
为了有更加准确的分割点,首先使用非线性自回归模型通过最小二乘法将刀盘转矩T的数据进行拟合,并通过程序测试不同阶次不同步长进行对比,选取其中误差最小的。

在确定模型结构后再从小到大测试不同的样本数据量,当分割点趋于平稳的时候就是最接近的分割点。
可以得出3种工况在模型结构是2阶,且1阶为2,2阶为1时误差最小,较为合理,并且数据变化情况表明数据有两个比较突变的情况。
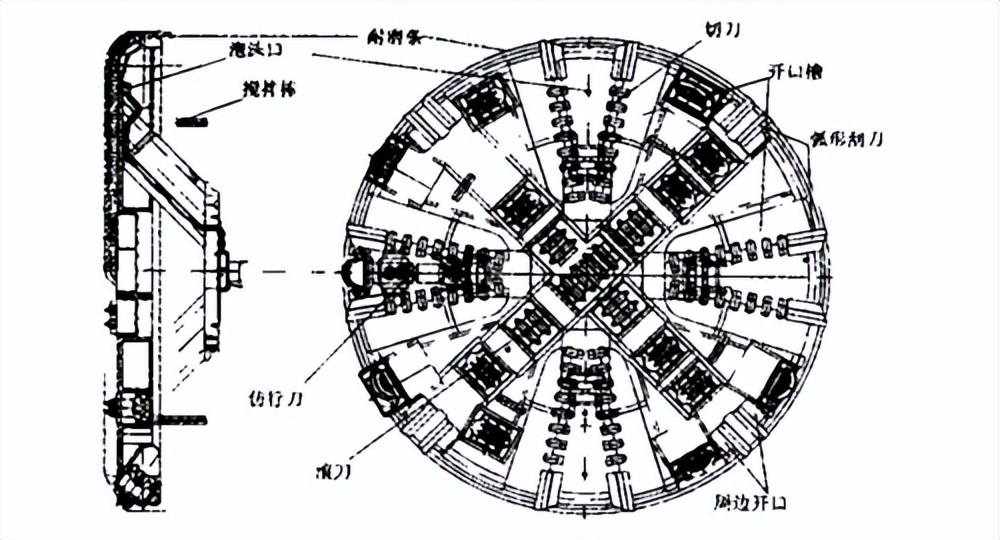
所以分割3段并选用此模型结构进行后面的分割,由于刀盘转矩T是最表现状态的数据,所以在进行多元分割的时候,也用此模型。
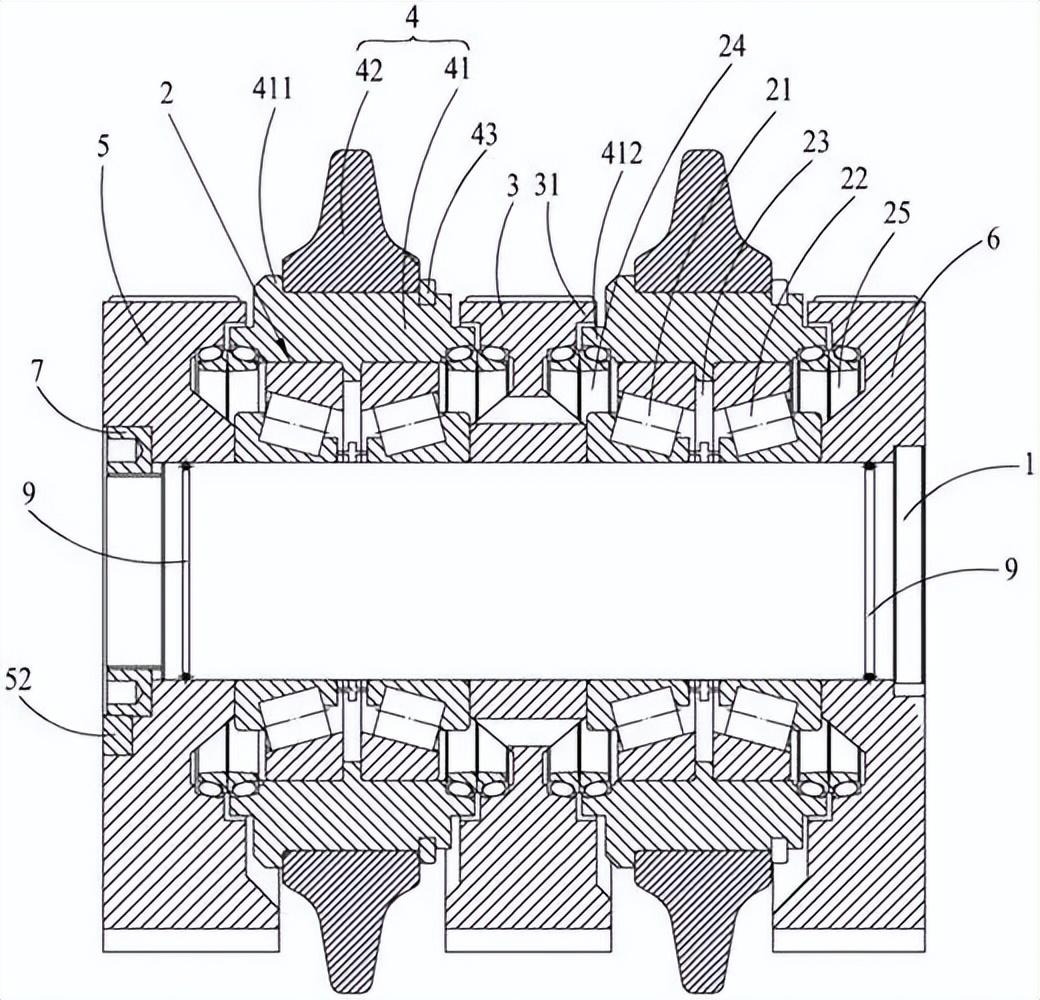
3.2试验结果
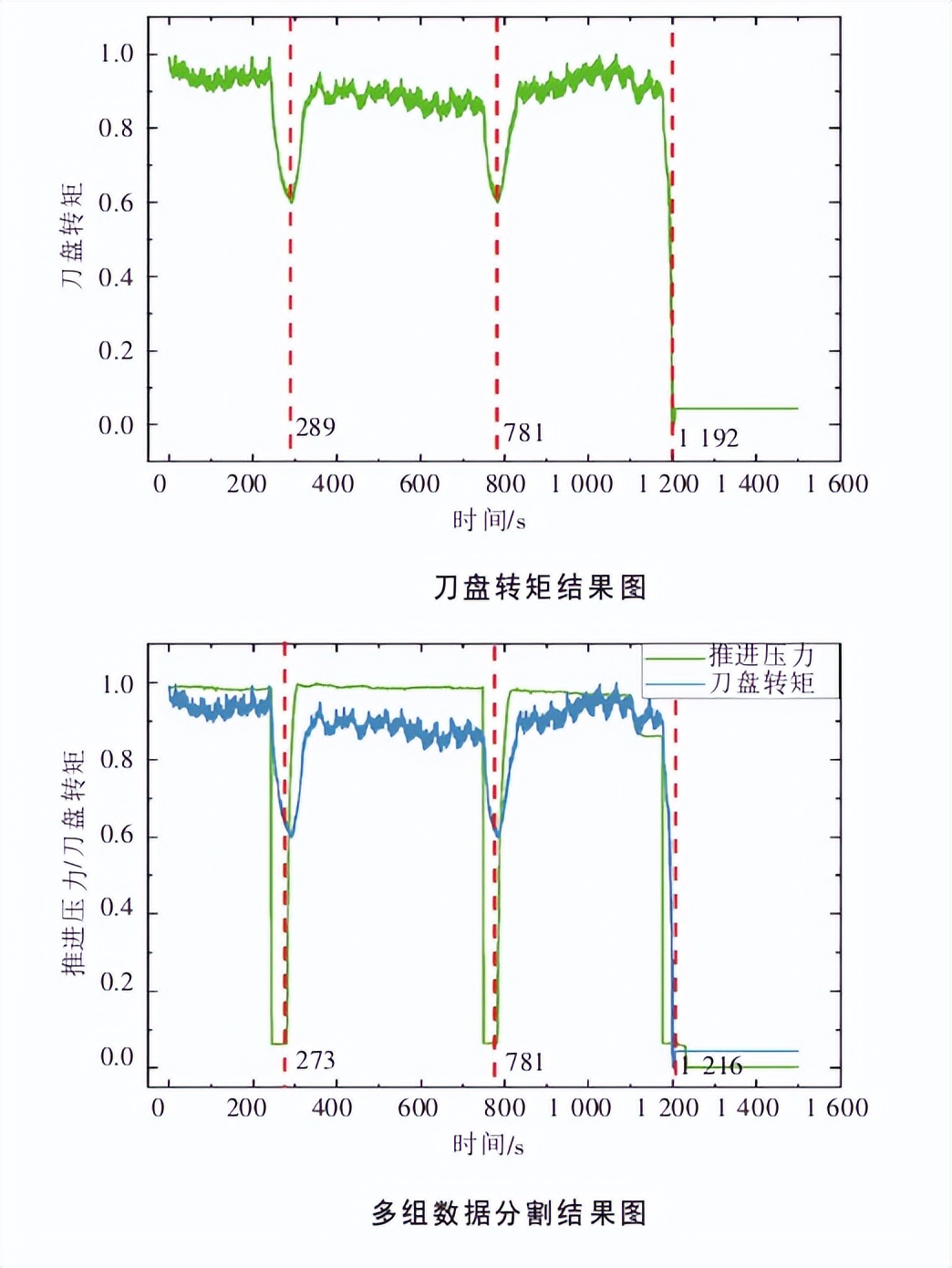
试验选用推进压力和刀盘转矩这两组数据进行分割试验,分别进行了单个数据的分割及两组数据多元分割,推进压力在特殊时刻瞬间下降,表示这个时候土地中有空鼓。
于此同时刀盘的转矩也随之下降,而下图所示的时间处进行分割时符合实际情况,所以此算法是有效的。
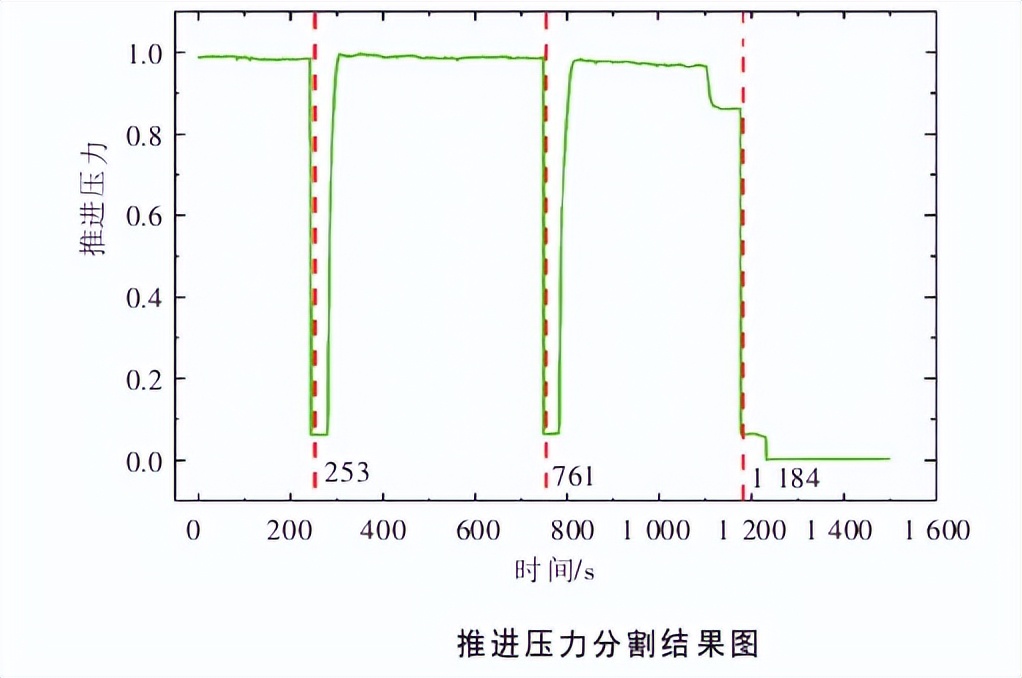
通过动态规划算法及多元非线性自回归算法的有机结合,建立了文中多元线性自回归时间序列分割的详细流程。
并根据多元线性自回归及动态规划原理通过python语言编写了多元非线性自回归动态规划算法程序,并通过4组时间函数试验检验所设计算法的性能。
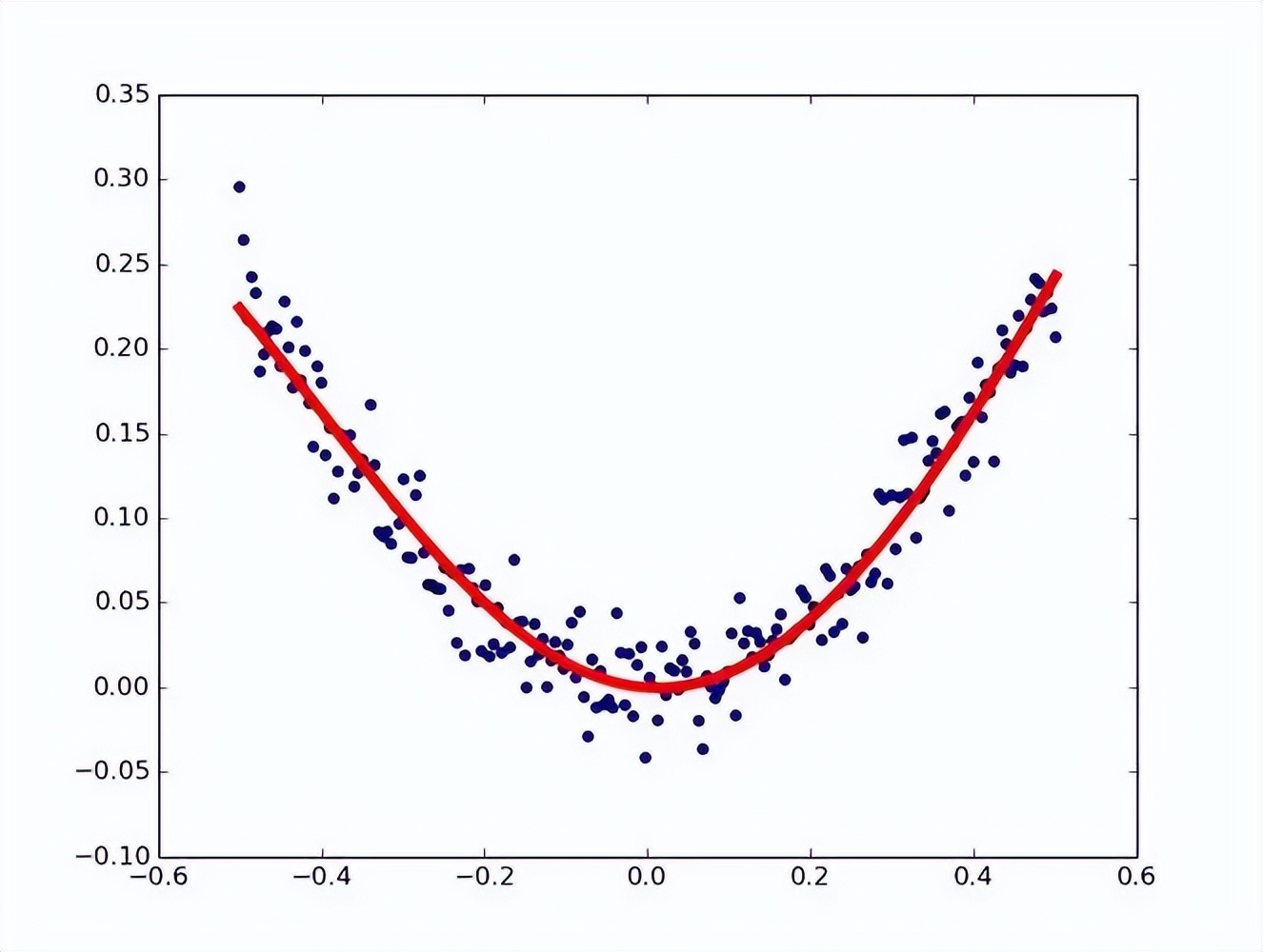
相比传统单一数据和线性分割拥有绝对的优势,将非线性自回归动态规划算法对3种工况下的盾构机数据进行分割,以刀盘转矩作为主要分割对象。
结合螺机转矩、A组推进位移这几组数据进行多元的分割,通过将数据图像进行对比,可知分割效果理想。

结论
文中介绍了一种基于非线性自回归的盾构机时间序列数据分割方法,该方法通过引入非线性的自回归关系,能够更准确地描述盾构机的运行状态.
实验结果表明,该方法在分割、分析和预测盾构机时间序列数据方面具有良好的性能,未来可以进一步改进与扩展该方法,以满足更高精度的盾构机状态识别与预测需求。
参考文献
[1]崔国华,王国强最小二乘法,何恩光.盾构机的研究现状及发展前景[J].矿山机械,2006,34(6):24-27.
[2]沈建奇,金先龙,王吉云.基于并行计算的盾构机过大堤三维数值模拟[J].上海交通大学学报,2008,42(8):1296-1300.
[3]杨宗金,薛亚东,张冬梅.TBM掘进机性能预测模型研究[C]//2016中国隧道与地下工程大会(CTUC)暨中国土木工程学会隧道及地下工程分会第十九届年会,成都,2016:540-546.
[4]姚宜斌,冉启顺,张豹.改进的启发式分割算法在GNSS坐标时间序列阶跃探测中的应用[J].武汉大学学报:信息科学版,2019,44(5):648-654.
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh