微积分的两个主要运算是微分(求曲线的斜率)和积分(求曲线下的面积)。微积分基本定理将这两个运算相互关联。它们本质上是互为逆的(在考虑积分常数之后)。
该定理分为两部分。微积分第一基本定理表明,积分本质上是微分的逆运算,换句话说,它是不定积分。微积分第二基本定理展示了如何计算定积分。
微积分第一基本定理
我们将函数的定积分写成如下形式:
我们使用变量t而不是x来表示这一点,原因稍后会解释清楚。变量名无关紧要,当然,定积分的值保持不变。
定积分表示t = a和t = b之间的曲线下的面积,如下所示:
现在假设我们不再使用常数b作为上限,而是将其设为变量。我们将其称为x。这样,定积分的值就依赖于x。也就是说,随着x值的变化,上限也会随之移动,因此曲线下的面积也会随之变化。
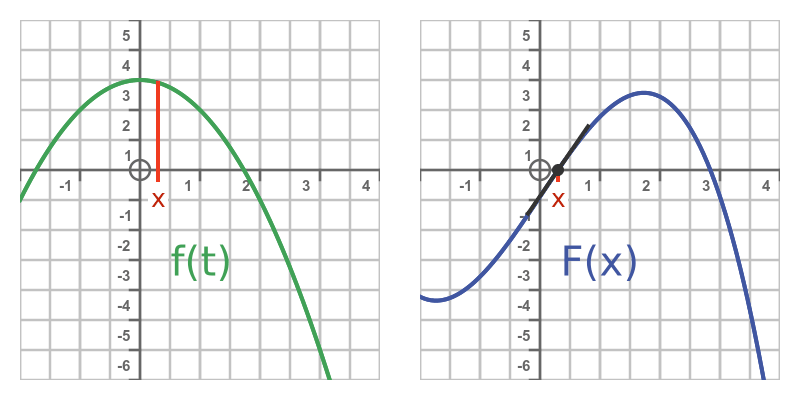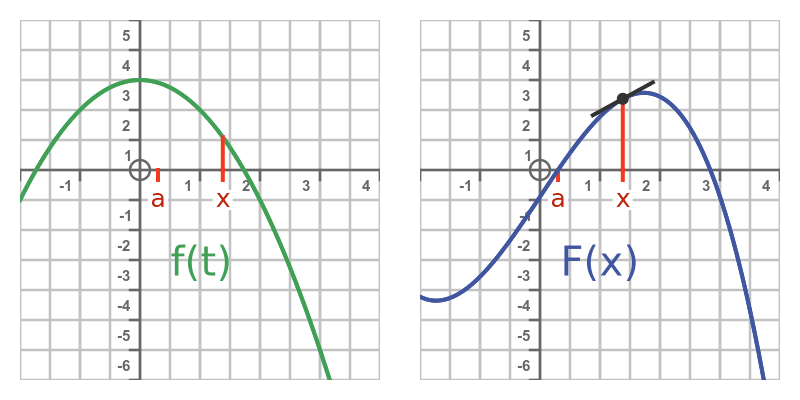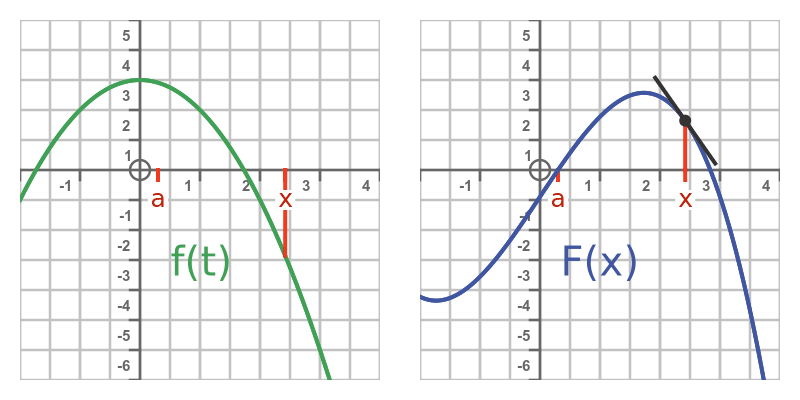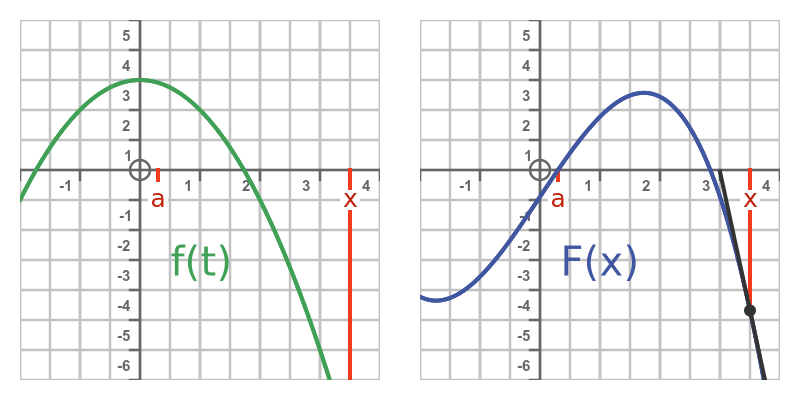
因此,我们可以将积分(即曲线下的面积)表示为x的函数:
这个想法如下所示。左侧曲线表示函数f。右侧曲线表示F。其值等于f图像上曲线下方的面积:
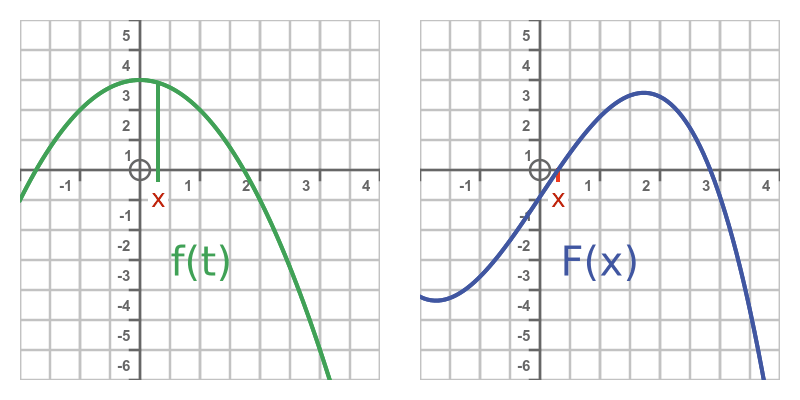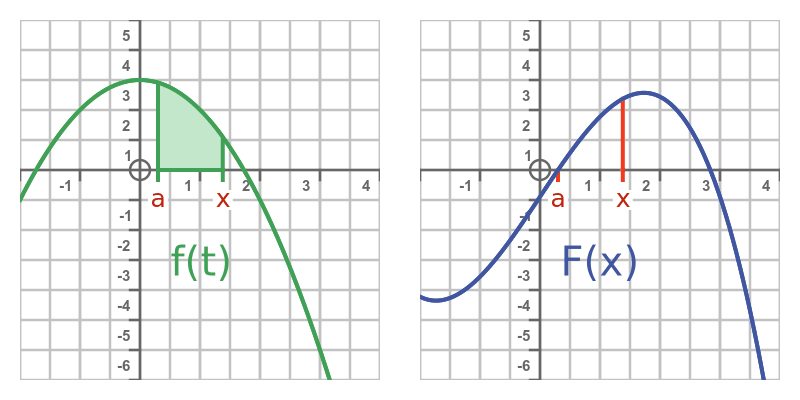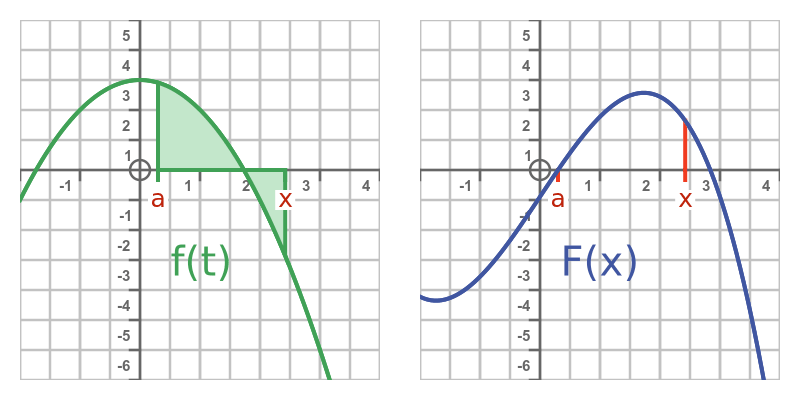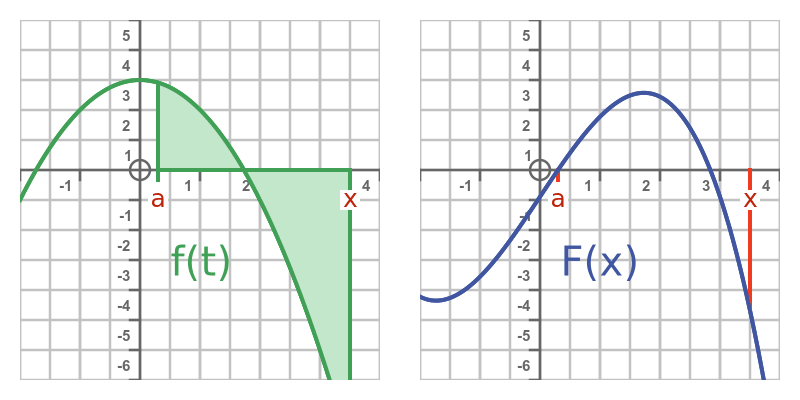
由于F(x)表示f(t)从任意点a到x的积分,因此意味着F实际上是f的不定积分。
现在我们进入重点部分,定理本身。这个定理并非自动从我们目前为止所说的内容推导出来,它需要被证明(我们很快就会证明)。这个定理可以表述如下:
这告诉我们,如果F是f的积分,那么f就是F的导数。这个重要定理将微分和积分联系起来。
它告诉我们, f的积分等于f的不定积分,其中不定积分是可以求f 的导数的函数。这意味着积分和微分是逆过程。
此动画显示了随着x 的增加,F的斜率与f下的面积的关系:
请注意:
微积分第二基本定理
第二定理与求定积分有关。它告诉我们:
这里,F再次表示为f的不定积分。这是一个重要的等式。它使我们能够计算点a和b之间曲线f下的面积微积分基本定理,只需对a和b两个值求不定积分F即可:
寻找不定积分
这些定理强调了积分的一个共同特征,我们在开始学习微积分时很早就学到了这一点。
通常可以通过第一性原理求出函数的导数,但这对积分来说却很少见。大多数已知的标准积分都是通过求已知导数的逆而发现的。
例如,如果我们想要整合如下表达式:
我们需要预先知道一个适用的不定积分。在本例中,我们知道:
因此我们可以找到需要微分才能得到x 的4 次方的东西:
这使我们能够解出积分:
距离/速度示例
作为一个直观的例子,考虑一辆手推车沿着平坦的表面直线滚动,如下所示:

这辆手推车以每秒1米的恒定速度v行驶。因此,6秒后,它行驶的距离s为6米:
在这个简单的例子中,距离图的斜率等于速度图的值。我们不需要微积分就能计算出来,它是恒定速度的基本运动方程。
现在我们来考虑一辆随时间变化速度的电车的情况。它一开始的速度很慢,2 秒后,速度阶跃变为一个更高的值,再过 2 秒,速度又阶跃变为一个更高的值:

速度和距离图表现在如下所示:
如果仔细观察,你会发现距离图有3个线性部分。在每个部分中,距离图的斜率等于速度图的幅值。
如果我们改变运动,使速度以 6 步变化,则图形如下所示:
这次,距离图有 6 个线性段,斜率也等于当时的速度值。但这次线性段不那么明显。
很容易想象,如果我们继续增加步数,直到速度函数平滑,那么距离曲线的斜率仍然会与每个时间点的速度曲线的值相匹配。
第一定理的证明
我们之前研究过第一定理的一个相当宽泛的定义。这里我们可以更精确地表述它。设f(x)是在区间 [a,b] 上连续的函数,我们可以将F(x)定义为:
该定理指出,对于x在 [a,b] 中,下列结论成立:
让我们从一阶导数的标准定义开始:
根据F(x)的先前定义,我们得到:
我们可以将这些项代入导数方程:
如果我们看这两个定积分,一个的范围从a到(x + h),另一个的范围从x到a。如果我们用一个积分减去另一个积分,就剩下从x到(x + h) 的积分:
我们可以将积分中值定理应用于此公式。该定理告诉我们,如果f(x)在区间 [a,b] 上连续,则在 [a,b] 中存在一个值c ,满足:
在我们的例子中,a等于x,b等于(x + h),所以(b — a)当然就是h。因此微积分基本定理,我们可以应用中值定理得出:
因此我们可以这样写F'(x) :
正如我们之前提到的,中值定理指出c在区间 [a,b] 内,在我们的例子中是区间 [x,x + h]。当h趋向于 0 时,该区间趋向于 [x,x],因此在极限下,c趋向于x。所以我们有:
这就证明了该定理。
第二定理的证明
我们再次从第二个定理的更严格表述开始:如果f(x)是在区间 [a,b]上连续的函数,且F(x)是f(x)的任何不定积分,则可以通过以下方式找到定积分:
顺便说一句,请注意这适用于f(x)的任何反导数。这是因为,如果F(x)是f(x)的反导数,那么将任何积分常数C添加到F(x)上也会产生f(x)的反导数。但是,因为我们是从F(b)中减去F(a),所以任何常数项都会消失。
为了证明这个定理,我们首先将区间 [a,b]分成n 个相等的子区间,如下所示:
边界 0 位于a处,边界n位于b处,边界 1 至(n — 1)在它们之间等距分布:
使用这个方案,我们可以将原始方程的 RHS 表示为:
现在我们来做一个小技巧:
注意我们在这里做了什么。我们在(n - 1)中添加了两个项,一个负数和一个正数,所以它们抵消为 0。我们还在(n - 2)中添加了两个项,一个负数和一个正数,它们也抵消为 0。以此类推。由于所有额外的项都被抵消,这个等式与上一个等式相同。
所以现在我们可以对这些术语进行不同的分组(这与以前是相同的表达,我们只是移动了括号):
这样做的原因是为了让我们可以将其写成一个总和:
接下来,我们将使用中值定理。这与我们之前使用的积分中值定理密切相关,它指出在区间 [u,v ] 中存在某个值c ,使得下列结论成立:
我们可以将其应用于上述 sigma 下的每个术语:
我们在第二行简化了这一过程,用 f(x) 代替F'(x)(我们知道它们在前面是等价的)。而且由于所有x值的间距都是等大的,我们可以直接用 Δx 来表示差值(它与i无关)。所以所有这些项的和是:
这个总和等于这些矩形的面积之和:
当n趋向无穷大时,Δx 趋向于 0,面积将趋向于f(x)的定积分。这证明了:
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh