二叉树遍历-数据结构——二叉树后序遍历（递归与非递归）

后序遍历思想

二叉树后序遍历的思想是： 1） 访问左子树；2） 访问右子树；3） 访问根结点。

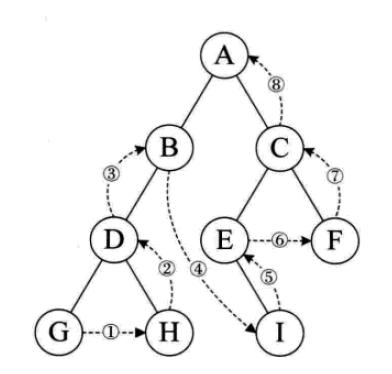
图1 二叉树后序遍历

图1遍历的顺序为：。

算法实现

【递归算法】

二叉树的后序遍历采用的是递归思想：

#include 
#include 
#define ElemType char
typedef struct BiTNode
{
  ElemType data;	//数据域
  struct BiTNode* lchild, * rchild;		//左右孩子指针
}BiTNode, * BiTree;
//构建树的函数
void CreateBiTree(BiTree* Tree)
{
  *Tree = (BiTNode*)malloc(sizeof(BiTNode));
  /*第一层*/
  (*Tree)->data = 'A';
  (*Tree)->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  /*第二层*/
  (*Tree)->lchild->data = 'B';
  (*Tree)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->lchild->rchild = NULL;
  (*Tree)->rchild->data = 'C';
  (*Tree)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  /*第三层*/
  (*Tree)->lchild->lchild->data = 'D';
  (*Tree)->lchild->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->lchild->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild->lchild->data = 'E';
  (*Tree)->rchild->lchild->lchild = NULL;
  (*Tree)->rchild->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild->rchild->data = 'F';
  (*Tree)->rchild->rchild->lchild = NULL;
  (*Tree)->rchild->rchild->rchild = NULL;
  /*第四层*/
  (*Tree)->lchild->lchild->lchild->data = 'G';
  (*Tree)->lchild->lchild->lchild->lchild = NULL;
  (*Tree)->lchild->lchild->lchild->rchild = NULL;
  (*Tree)->lchild->lchild->rchild->data = 'H';
  (*Tree)->lchild->lchild->rchild->lchild = NULL;
  (*Tree)->lchild->lchild->rchild->rchild = NULL;
  (*Tree)->rchild->lchild->rchild->data = 'I';
  (*Tree)->rchild->lchild->rchild->lchild = NULL;
  (*Tree)->rchild->lchild->rchild->rchild = NULL;
}
//模拟操作结点元素的函数，输出结点本身的数值
void DisplayElem(BiTNode* elem)
{
  std::cout <data <lchild);
    ProOrderTraverse(T->rchild);
    DisplayElem(T);
  }
}
/*主函数*/
int main()
{
  BiTree Tree;
  CreateBiTree(&Tree);
  std::cout << "后序遍历" << std::endl;
  ProOrderTraverse(Tree);
  std::cout << std::endl;
  return 0;
}

【非递归算法】

递归的实现过程是依靠栈存储结构，因此可以申请一块内存模拟递归的过程。后序非递归遍历中，访问根（子根）结点有两种情况

基于这个特性，我们需要区分二叉树遍历，到底这个根结点，是访问完了左子树还是右子树二叉树遍历，所以需要添加一个变量帮助辨认。

#include 
#include 
#include 
#define ElemType char
typedef struct BiTNode
{
  ElemType data;	//数据域
  struct BiTNode* lchild, * rchild;		//左右孩子指针
}BiTNode, * BiTree;
//构建树的函数
void CreateBiTree(BiTree* Tree)
{
  *Tree = (BiTNode*)malloc(sizeof(BiTNode));
  /*第一层*/
  (*Tree)->data = 'A';
  (*Tree)->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  /*第二层*/
  (*Tree)->lchild->data = 'B';
  (*Tree)->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->lchild->rchild = NULL;
  (*Tree)->rchild->data = 'C';
  (*Tree)->rchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  /*第三层*/
  (*Tree)->lchild->lchild->data = 'D';
  (*Tree)->lchild->lchild->lchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->lchild->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild->lchild->data = 'E';
  (*Tree)->rchild->lchild->lchild = NULL;
  (*Tree)->rchild->lchild->rchild = (BiTNode*)malloc(sizeof(BiTNode));
  (*Tree)->rchild->rchild->data = 'F';
  (*Tree)->rchild->rchild->lchild = NULL;
  (*Tree)->rchild->rchild->rchild = NULL;
  /*第四层*/
  (*Tree)->lchild->lchild->lchild->data = 'G';
  (*Tree)->lchild->lchild->lchild->lchild = NULL;
  (*Tree)->lchild->lchild->lchild->rchild = NULL;
  (*Tree)->lchild->lchild->rchild->data = 'H';
  (*Tree)->lchild->lchild->rchild->lchild = NULL;
  (*Tree)->lchild->lchild->rchild->rchild = NULL;
  (*Tree)->rchild->lchild->rchild->data = 'I';
  (*Tree)->rchild->lchild->rchild->lchild = NULL;
  (*Tree)->rchild->lchild->rchild->rchild = NULL;
}
//模拟操作结点元素的函数，输出结点本身的数值
void DisplayElem(BiTNode* elem)
{
  std::cout <data << " ";
}
/*后序遍历*/
void ProOrderTraverse(BiTree T)
{
  std::stack sta;
  BiTNode* top = T;
  BiTNode* vis = nullptr;/*临时变量，记录上一个访问到的结点，因为从右边访问根结点，
  																		必定是右子树已经遍历结束，此时上一个访问的结点必定是右子树的根结点*/
  while (top || !sta.empty())
  {
    if (top)
    {
      sta.push(top);
      top = top->lchild;
    }
    else
    {
      top = sta.top();//只读取根结点，不对栈内结点进行操作
      if (top->rchild && top->rchild != vis)//没有对右子树进行操作过
      {
        top = top->rchild;
        sta.push(top);
        top = top->lchild;
      }
      else
      {
        sta.pop();
        DisplayElem(top);//对top进行访问，可以进行打印等操作
        vis = top;//记录当前访问的是p结点
        top = nullptr;//把p置空，进入下一次循环，直到栈内无元素，且p为空时遍历完成
      }
    }
  }
}
/*主函数*/
int main()
{
  BiTree Tree;
  CreateBiTree(&Tree);
  std::cout << "后序遍历" << std::endl;
  ProOrderTraverse(Tree);
  std::cout << std::endl;
  return 0;
}

完整代码

: %

限时特惠:本站持续每日更新海量各大内部创业课程，一年会员仅需要98元，全站资源免费下载
点击查看详情

站长微信:Jiucxh