动态规划背包问题-【动态规划/背包问题】分组背包问题

前言

今天是我们讲解「动态规划专题」中的「背包问题」的第十二篇。

今天将会学习「分组背包」问题。

另外，我在文章结尾处列举了我所整理的关于背包问题的相关题目。

背包问题我会按照编排好的顺序进行讲解（每隔几天更新一篇，确保大家消化）。

你也先可以尝试做做，也欢迎你向我留言补充，你觉得与背包相关的 DP 类型题目 ~

分组背包

给定个物品组，和容量为的背包。

第个物品组共有件物品，其中第组的第件物品的成本为动态规划背包问题，价值为。

每组有若干个物品，同一组内的物品最多只能选一个。

求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

示例：

输入：N = 2, C = 9, S = [2, 3], v = [[1,2,-1],[1,2,3]], w = [[2,4,-1],[1,3,6]]

输出：10

提示：

基本分析

从题面看，这似乎是一种全新的背包问题。

但其仍然是一种通过「枚举物品 - 枚举容量 - 枚举决策」来解决的组合优化问题。

经过之前的学习。

我们可以很轻松给出状态定义：定义为考虑前个物品组，背包容量不超过的最大价值。

不失一般性的考虑如何计算。

由于每组有若干个物品动态规划背包问题，且每组「最多」选择一件物品。

即对于第组而言，可决策的方案如下：

...

显然最终的应该是从所有方案里取：

代码：

class Solution {
    public int maxValue(int N, int C, int[] S, int[][] v, int[][] w) {
        int[][] dp = new int[N + 1][C + 1];
        for (int i = 1; i <= N; i++) {
            int[] vi = v[i - 1];
            int[] wi = w[i - 1];
            int si = S[i - 1];
            for (int j = 1; j <= C; j++) {
                dp[i][j] = dp[i - 1][j];
                for (int k = 0; k < si; k++) {
                    if (j >= vi[k]) {
                        dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - vi[k]] + wi[k]);
                    }
                }
            }
        }
        return dp[N][C];
    }
}

空间优化滚动数组

根据状态转移方程，不难发现只依赖于，且 = x" data--type="-" style="">。

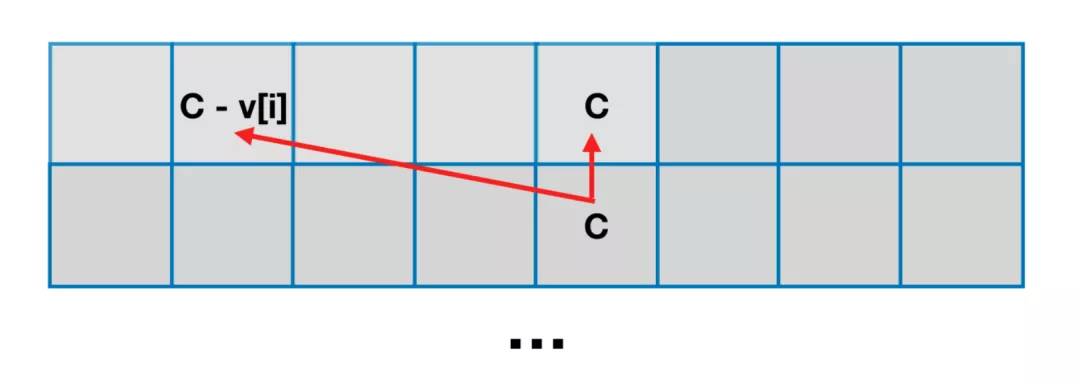
动态规划之背包问题_动态规划背包问题算法分析_动态规划背包问题

即明确只依赖上一物品组的决策结果。

因此，我们可以使用就学过的「滚动数组」的方式，十分机械的将的空间优化到。

代码：

class Solution {
    public int maxValue(int N, int C, int[] S, int[][] v, int[][] w) {
        int[][] dp = new int[2][C + 1];
        for (int i = 1; i <= N; i++) {
            int[] vi = v[i - 1];
            int[] wi = w[i - 1];
            int si = S[i - 1];
            for (int j = 1; j <= C; j++) {
                int a = i & 1, b = (i - 1) & 1;
                dp[a][j] = dp[b][j];
                for (int k = 0; k < si; k++) {
                    if (j >= vi[k]) {
                        dp[a][j] = Math.max(dp[a][j], dp[b][j - vi[k]] + wi[k]);
                    }
                }
            }
        }
        return dp[N & 1][C];
    }
}

一维空间优化

进一步，我们可以用「01 背包」类似的思路，进行一维空间优化：

取消物品维度；

将容量维度的遍历顺序修改为「从大到小」（确保所依赖的值不会被覆盖）。

代码：

class Solution {
    public int maxValue(int N, int C, int[] S, int[][] v, int[][] w) {
        int[] dp = new int[C + 1];
        for (int i = 1; i <= N; i++) {
            int[] vi = v[i - 1];
            int[] wi = w[i - 1];
            int si = S[i - 1];
            for (int j = C; j >= 0; j--) {
                for (int k = 0; k < si; k++) {
                    if (j >= vi[k]) {
                        dp[j] = Math.max(dp[j], dp[j - vi[k]] + wi[k]);
                    }
                }
            }
        }
        return dp[C];
    }
}