排序法-动画详解常用排序算法（1）

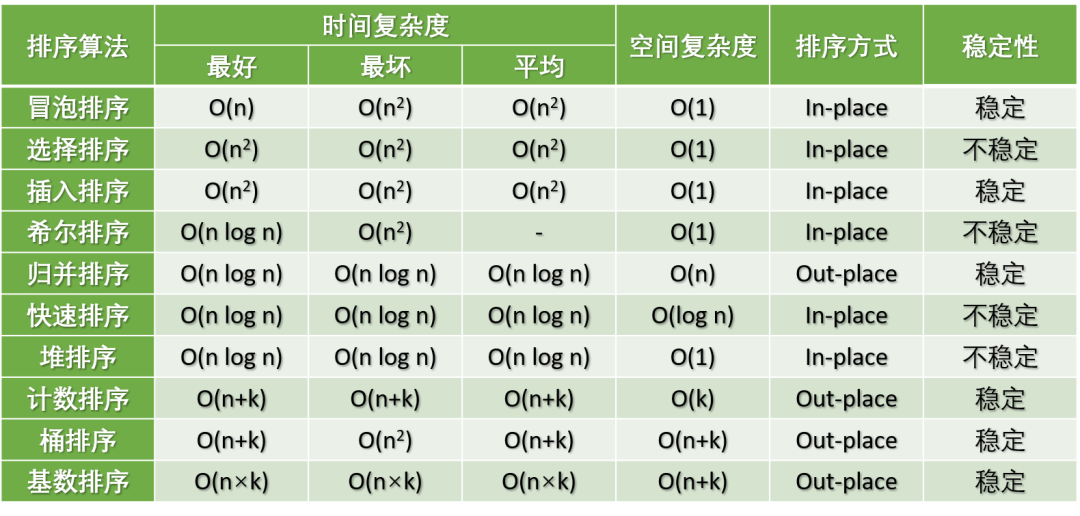
排序算法是一类非常经典的算法，说来简单，说难也难。刚学编程时大家都爱用冒泡排序，随后接触到选择排序、插入排序等，历史上还有昙花一现的希尔排序，公司面试时也经常会问到快速排序等等，小小的排序算法，融入了无数程序大牛的心血。

如牛顿所言，正是站在巨人的肩膀上，我们才能望得更远。本文我们就来一起梳理一下排序算法的前世今生。

冒泡排序

冒泡排序是入门级的算法，但也有一些有趣的玩法。通常来说，冒泡排序有三种写法：

1.1 冒泡排序的第一种写法

代码如下：

public static void bubbleSort(int[] arr) {    for (int i = 0; i < arr.length - 1; i++) {        for (int j = 0; j < arr.length - 1 - i; j++) {            if (arr[j] > arr[j + 1]) {                // 如果左边的数大于右边的数，则交换，保证右边的数字最大                arr[j + 1] = arr[j + 1] + arr[j];                arr[j] = arr[j + 1] - arr[j];                arr[j + 1] = arr[j + 1] - arr[j];            }        }    }}

最外层的 for 循环每经过一轮，剩余数字中的最大值就会被移动到当前轮次的最后一位，中途也会有一些相邻的数字经过交换变得有序。总共比较次数是(n-1)+(n-2)+(n-3)+…+1。

这种写法相当于相邻的数字两两比较，并且规定：“谁大谁站右边”。经过 n-1 轮，数字就从小到大排序完成了。整个过程看起来就像一个个气泡不断上浮，这也是“冒泡排序法”名字的由来。

其中，我们在交换两个数字时使用了一个小魔术：没有引入第三个中间变量就完成了两个数字的交换。这个交换问题曾经出现在大厂面试题中，感兴趣的读者可以细品一下。除了这种先加后减的写法，还有一种先减后加的写法：

arr[j + 1] = arr[j] - arr[j + 1];arr[j] = arr[j] - arr[j + 1];arr[j + 1] = arr[j + 1] + arr[j];

这两种交换数字的方式和我们平时常用的写法是等价的（不考虑数字越界的情况）：

int temp = arr[j + 1];arr[j + 1] = arr[j];arr[j] = temp;

1.2 冒泡排序的第二种写法

第二种写法是在第一种写法的基础上改良而来的：

public static void bubbleSort(int[] arr) {    // 初始时 swapped 为 true，否则排序过程无法启动    boolean swapped = true;    for (int i = 0; i < arr.length - 1; i++) {        // 如果没有发生过交换，说明剩余部分已经有序，排序完成        if (!swapped) break;        // 设置 swapped 为 false，如果发生交换，则将其置为 true        swapped = false;        for (int j = 0; j < arr.length - 1 - i; j++) {            if (arr[j] > arr[j + 1]) {                // 如果左边的数大于右边的数，则交换，保证右边的数字最大                int temp = arr[j];                arr[j] = arr[j + 1];                arr[j + 1] = temp;                // 表示发生了交换                swapped = true;            }        }    }}

最外层的 for 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。这种写法相对于第一种写法的优点是：如果一轮比较中没有发生过交换，则立即停止排序，因为此时剩余数字一定已经有序了。

看下动图演示：

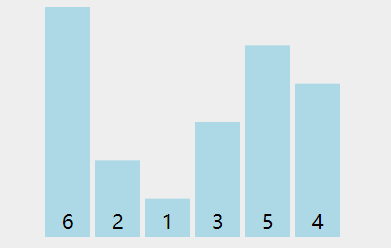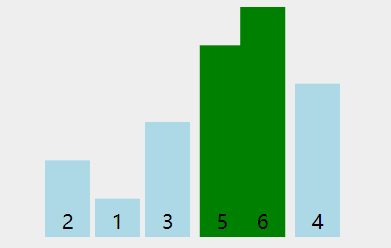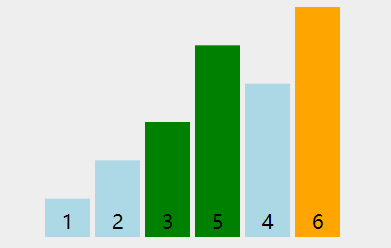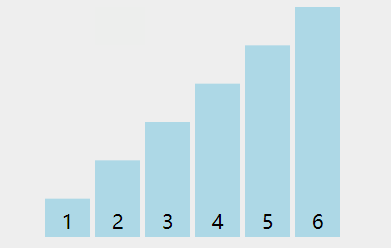
图中可以看出：

1.3 冒泡排序的第三种写法

第三种写法比较少见，它是在第二种写法的基础上进一步优化：

public static void bubbleSort(int[] arr) {    boolean swapped = true;    // 最后一个没有经过排序的元素的下标    int indexOfLastUnsortedElement = arr.length - 1;    // 上次发生交换的位置    int swappedIndex = -1;    while (swapped) {        swapped = false;        for (int i = 0; i < indexOfLastUnsortedElement; i++) {            if (arr[i] > arr[i + 1]) {                // 如果左边的数大于右边的数，则交换，保证右边的数字最大                int temp = arr[i];                arr[i] = arr[i + 1];                arr[i + 1] = temp;                // 表示发生了交换                swapped = true;                // 更新交换的位置                swappedIndex = i;            }        }        // 最后一个没有经过排序的元素的下标就是最后一次发生交换的位置        indexOfLastUnsortedElement = swappedIndex;    }}

经过再一次的优化，代码看起来就稍微有点复杂了。最外层的 while 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。

在下一轮比较时，只需比较到上一轮比较中，最后一次发生交换的位置即可。因为后面的所有元素都没有发生过交换，必然已经有序了。

当一轮比较中从头到尾都没有发生过交换，则表示整个列表已经有序，排序完成。

测试：

public void test() {    int[] arr = new int[]{6, 2, 1, 3, 5, 4};    bubbleSort(arr);    // 输出: [1, 2, 3, 4, 5, 6]    System.out.println(Arrays.toString(arr));}

冒泡排序从 1956 年就有人开始研究，之后经历过多次优化。它的空间复杂度为 O(1)，时间复杂度为 O(n^2)，第二种、第三种冒泡排序由于经过优化，最好的情况下只需要 O(n) 的时间复杂度。

最好情况：在数组已经有序的情况下，只需遍历一次，由于没有发生交换，排序结束。

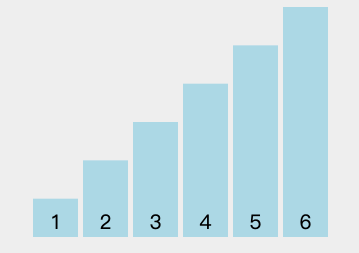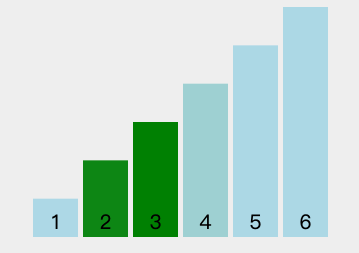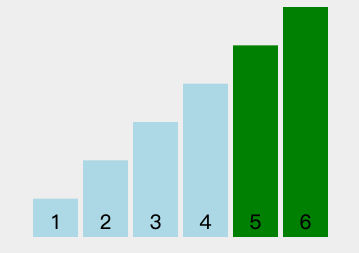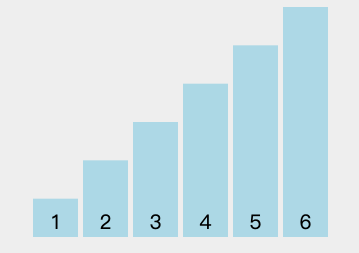
最差情况：数组顺序为逆序，每次比较都会发生交换。

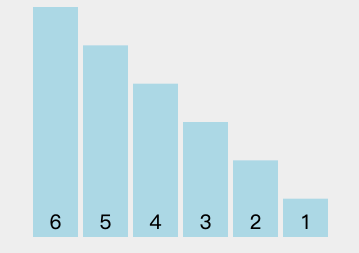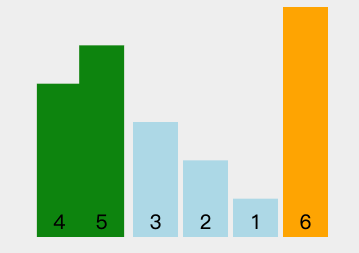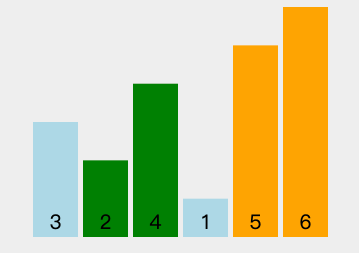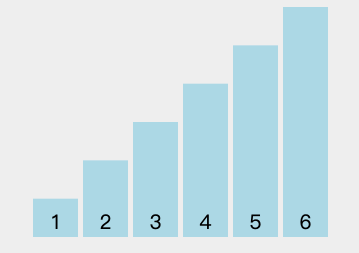
但优化后的冒泡排序平均时间复杂度仍然是 O(n^2)，所以这些优化对算法的性能并没有质的提升。正如 E. Knuth（1974 年图灵奖获得者）所言：“冒泡排序法除了它迷人的名字和导致了某些有趣的理论问题这一事实外，似乎没有什么值得推荐的。”

不管怎么说，冒泡排序法是所有排序算法的老祖宗，如同程序界经典的 “Hello, world” 一般经久不衰，总是出现在各类算法书刊的首个章节。但面试时如果你说你只会冒泡排序可就太掉价了，接下来我们就来认识一下他的继承者们。

选择排序

选择排序的思想是：双重循环遍历数组，每经过一轮比较，找到最小元素的下标，将其交换至首位。

public static void selectionSort(int[] arr) {    int minIndex;    for (int i = 0; i < arr.length - 1; i++) {        minIndex = i;        for (int j = i + 1; j < arr.length; j++) {            if (arr[minIndex] > arr[j]) {                // 记录最小值的下标                minIndex = j;            }        }        // 将最小元素交换至首位        int temp = arr[i];        arr[i] = arr[minIndex];        arr[minIndex] = temp;    }}

选择排序就好比第一个数字站在擂台上，大吼一声：“还有谁比我小？”。剩余数字来挨个打擂，如果出现比第一个数字小的数，则新的擂主产生。每轮打擂结束都会找出一个最小的数，将其交换至首位。经过 n-1 轮打擂，所有的数字就按照从小到大排序完成了。

动图演示：

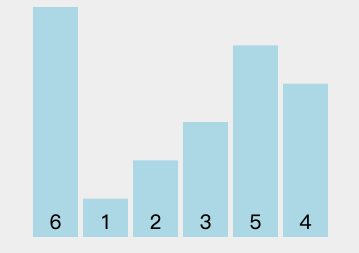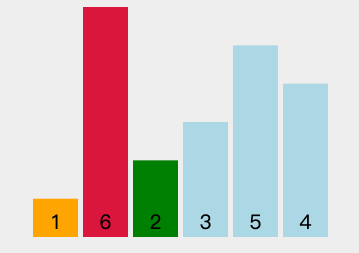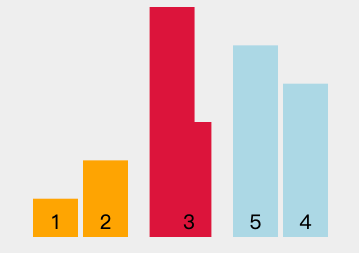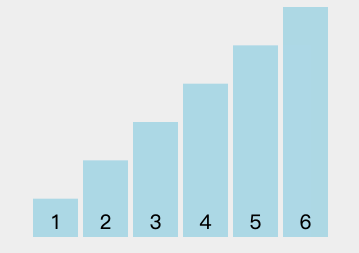
图中可以看出，每一轮排序都找到了当前的最小值排序法，这个最小值就是被选中的数字，将其交换至本轮首位。这就是“选择排序法”名称的由来。

由于选择排序法交换次数较少，所以整个排序过程看起来是非常清爽的，类似这样：

正是由于它比较容易理解排序法，许多初学者在排序时非常喜欢使用选择排序法。

现在让我们思考一下，冒泡排序和选择排序有什么异同？

相同点：

不同点：

事实上，冒泡排序和选择排序还有一个非常重要的不同点，那就是：

想要理解这点不同，我们先要知道什么是排序算法的稳定性：

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。

理解了稳定性的定义后，我们就能分析出：冒泡排序中，只有左边的数字大于右边的数字时才会发生交换，相等的数字之间不会发生交换，所以它是稳定的。

而选择排序中，最小值和首位交换的过程可能会破坏稳定性。比如数列：[2, 2, 1]，在选择排序中第一次进行交换时，原数列中的两个 2 的相对顺序就被改变了，因此，我们说选择排序是不稳定的。

那么排序算法的稳定性有什么意义呢？其实它只在一种情况下有意义：当要排序的内容是一个对象的多个数字属性，且其原本的顺序存在意义时，如果我们需要在二次排序后保持原有排序的意义，就需要使用到稳定性的算法。

举个例子，如果我们要对一组商品排序，商品存在两个属性：价格和销量。当我们按照价格从高到低排序后，要再按照销量对其排序，这时，如果要保证销量相同的商品仍保持价格从高到低的顺序，就必须使用稳定性算法。

2.1 二元选择排序

选择排序算法也是可以优化的，既然每轮遍历时找出了最小值，何不把最大值也顺便找出来呢？这就是二元选择排序的思想。

使用二元选择排序，每轮选择时记录最小值和最大值，可以把选择排序的效率提升一倍。

public static void selectionSort2(int[] arr) {    int minIndex, maxIndex;    // i 只需要遍历一半    for (int i = 0; i < arr.length / 2; i++) {        minIndex = i;        maxIndex = i;        for (int j = i + 1; j < arr.length - i; j++) {            if (arr[minIndex] > arr[j]) {                // 记录最小值的下标                minIndex = j;            }            if (arr[maxIndex] < arr[j]) {                // 记录最大值的下标                maxIndex = j;            }        }        // 将最小元素交换至首位        int temp = arr[i];        arr[i] = arr[minIndex];        arr[minIndex] = temp;        // 如果最大值的下标刚好是 i，由于 arr[i] 和 arr[minIndex] 已经交换了，所以这里要更新 maxIndex 的值。        if (maxIndex == i) maxIndex = minIndex;        // 将最大元素交换至末尾        int lastIndex = arr.length - 1 - i;        temp = arr[lastIndex];        arr[lastIndex] = arr[maxIndex];        arr[maxIndex] = temp;    }}

我们使用 记录最小值的下标， 记录最大值的下标。每次遍历后，将最小值交换到首位，最大值交换到末尾，就完成了排序。

由于每一轮遍历可以排好两个数字，所以最外层的遍历只需遍历一半即可。

二元选择排序中有一句很重要的代码，它位于交换最小值和交换最大值的代码中间：

if (maxIndex == i) maxIndex = minIndex;

这行代码的作用处理了一种特殊情况：如果最大值的下标等于 i，也就是说 arr[i] 就是最大值，由于 arr[i] 是当前遍历轮次的首位，它已经和 arr[] 交换了，所以最大值的下标需要跟踪到 arr[i] 最新的下标 。

经过优化之后，选择排序的效率提升了一倍。但可惜的是，这样的优化无法改变时间复杂度，我们知道时间复杂度与常量系数无关，O(n^2) 除以 2 仍然是 O(n^2)。

和选择排序一样，二元选择排序也是不稳定的。

插入排序

插入排序的思想非常简单，生活中有一个非常常见的场景：在打扑克牌时，我们一边抓牌一边给扑克牌排序，每次摸一张牌，就将它插入手上已有的牌中合适的位置，逐渐完成整个排序。

不打牌的好孩纸直接看代码：

public static void insertSort(int[] arr) {    // 从第二个数开始，往前插入数字    for (int i = 1; i < arr.length; i++) {        int currentNumber = arr[i];        int j = i - 1;        // 寻找插入位置的过程中，不断地将比 currentNumber 大的数字向后挪        while (j >= 0 && currentNumber < arr[j]) {            arr[j + 1] = arr[j];            j--;        }        // 两种情况会跳出循环：1. 遇到一个小于或等于 currentNumber 的数字，跳出循环，currentNumber 就坐到它后面。        // 2. 已经走到数列头部，仍然没有遇到小于或等于 currentNumber 的数字，也会跳出循环，此时 j 等于 -1，currentNumber 就坐到数列头部。        arr[j + 1] = currentNumber;    }}

当数字少于两个时，不存在排序问题，当然也不需要插入，所以我们直接从第二个数字开始往前插入。将当前的数字不断与前面的数字比较，寻找插入位置。

在比较的过程中，我们将大于当前数字的元素不断向后移动。这个过程就像是已经有一些数字坐成了一排，这时一个新的数字要加入，所以这一排数字不断地向后腾出位置，当新的数字找到自己合适的位置后，就可以直接坐下了。重复此过程，直到排序结束。

动图演示：

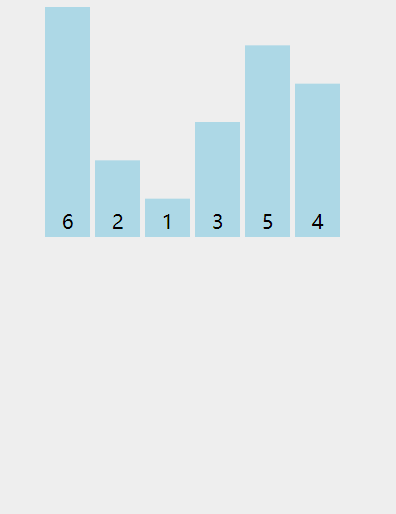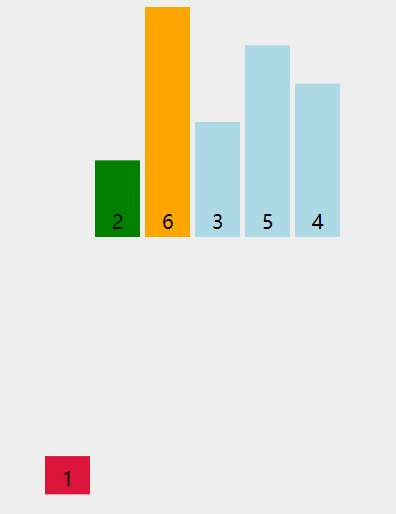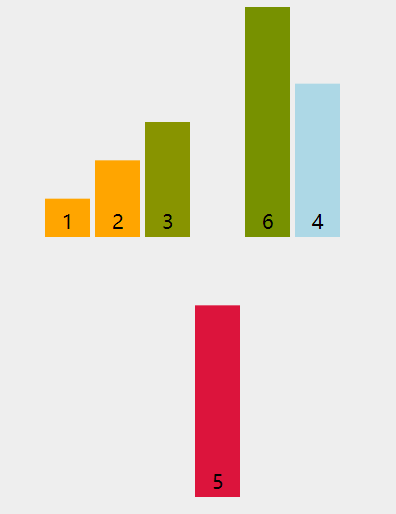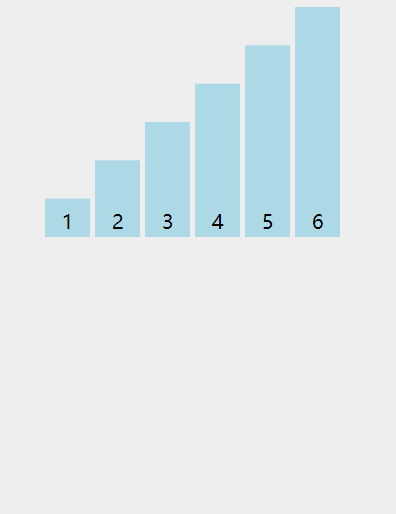
插入数据时，不仅可以用这种移动元素的方式，还可以使用交换元素的方式。代码如下：

public static void insertSort(int[] arr) {    // 从第二个数开始，往前插入数字    for (int i = 1; i < arr.length; i++) {        // j 记录当前数字下标        int j = i;        // 当前数字比前一个数字小，则将当前数字与前一个数字交换        while (j >= 1 && arr[j] < arr[j - 1]) {            int temp = arr[j];            arr[j] = arr[j - 1];            arr[j - 1] = temp;            // 更新当前数字下标            j--;        }    }}

这种方式就像是这个新加入的数字原本坐在一排数字的最后一位，然后它不断地与前面的数字比较，如果前面的数字比它大，它就和前面的数字交换位置。

分析可知，插入排序的过程不会破坏原有数组中相同关键字的相对次序，所以插入排序是一种稳定的排序算法。

本文介绍的排序算法都还比较容易理解，因为他们的思想和我们生活中的排序方式是非常类似的。遗憾的是他们的时间复杂度都是 O(n^2)，这是一个比较高的时间复杂度。程序界无数大牛在这些算法的基础上不断优化，仍然无法冲破 O(n^2) 的桎梏，直到 1959 年 7 月，美国辛辛那提大学的数学系博士 Shell 在 《ACM 通讯》上发表了希尔排序算法，人们才慢慢找到将排序的时间复杂度降下来的方式，我们将在下篇文章中介绍希尔排序的思想。

BY /

限时特惠:本站持续每日更新海量各大内部创业课程，一年会员仅需要98元，全站资源免费下载
点击查看详情

站长微信:Jiucxh