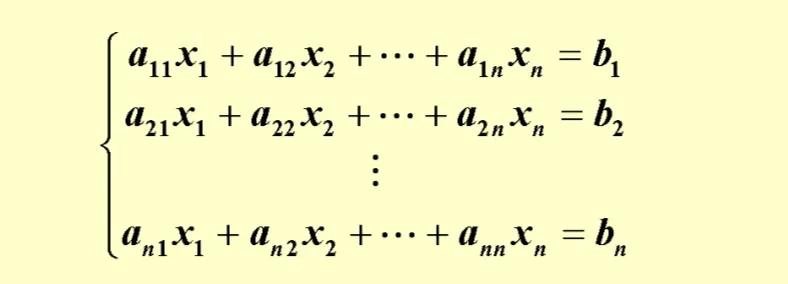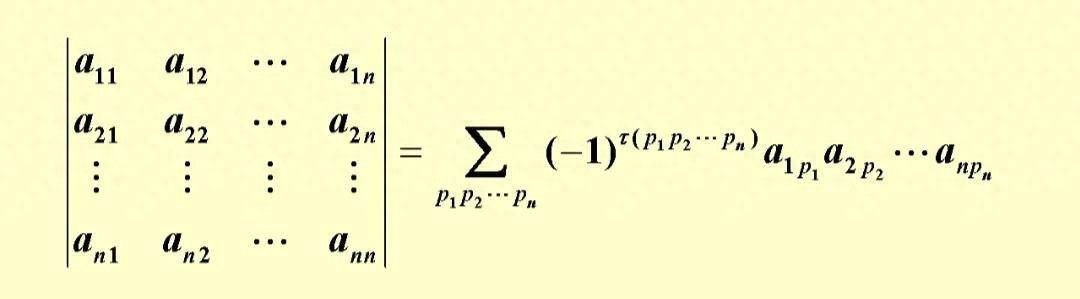行列式是线性代数中的一个基本概念,它在数学、物理、计算机科学等许多领域都有广泛的应用。本文将介绍行列式的定义、性质以及一些常见的应用。
一、定义
假设我们有一个n×n的矩阵A,它的元素为a_ij。那么,我们可以定义一个n!(n的阶乘)的函数,称之为行列式,记作det(A)或|A|。对于一个具体的矩阵A,我们可以通过以下公式计算其行列式:
|A| = …a_nn + (-1)^(1+2)…a_nn + … + (-1)^(n-1+n)…*a_n1
可以看出,行列式是将矩阵的元素按照一定的规律相乘,然后求和得到的结果。特别地,对于一个1×1的矩阵,其行列式就是它唯一的元素值;对于一个2×2的矩阵,其行列式是两个对角线元素的乘积减去两个非对角线元素的乘积。
二、性质
行列式具有以下重要性质:
1、线性性质:对于任意两个矩阵A和B,以及任意实数λ,有|λA + B| = λ^n |A| + |B|,其中n是矩阵的阶数。
2、三角行列式的性质:如果矩阵A的元素满足a_ij = 0行列式,当i > j时,那么|A| = …*a_nn。
3、列(行)交换性质:如果将矩阵A的第i列(行)与第j列(行)交换,那么|A| = -|A|。
4、列(行)倍性性质:如果将矩阵A的第i列(行)乘以λ,那么|A| = λ*|A|。
5、行列式的绝对值等于其转置矩阵的行列式:|A| = |A^T|。
三、应用
行列式在许多领域都有应用,以下列举一些常见的应用:
1、方程组的解:对于一个线性方程组,如果其系数矩阵的行列式不等于0,那么该方程组有唯一解。
2、反映几何变换:对于一个矩阵A,其行列式反映了由A所表示的线性变换对面积(体积)的影响。如果|A| > 0,那么A保持了面积(体积)的正向;如果|A| < 0,那么A改变了面积(体积)的正向。
3、逆矩阵:一个矩阵A的逆矩阵A^-1存在当且仅当|A| != 0。此时行列式,A^-1 = |A|^-1 * adj(A),其中adj(A)是A的伴随矩阵。
4、特征值和特征向量:矩阵A的特征值λ满足det(A - λI) = 0,其中I是单位矩阵。这个方程称为特征方程,它的解就是矩阵A的特征值。
总之,行列式是线性代数中的一个重要概念,它具有丰富的性质和广泛的应用。学习行列式有助于我们更好地理解和应用矩阵,从而解决各类实际问题。
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh