微分流形上的点不能直接求导的原因在于微分流形的定义和性质。
微分流形是一种带有微分结构的拓扑空间导数与微分,它是拓扑学和几何学中一类重要的空间。微分流形是三维欧式空间中曲线和曲面概念的推广,可以有更高的维数,但不必有距离和度量的概念。微分流形上的点不能直接求导,主要是因为微分流形上的函数定义和导数的定义与普通欧几里得空间中的定义有所不同。
也就是说,微分流形首先是一个拓扑空间,而拓扑空间首先强调的是这个空间中的元素可分离性质,是一种基于集合意义的定义。定义于微分流形上的函数,是一种对应关系,即把微分流形上的点与欧氏空间中的点对应起来,因为微分流形不具备坐标系,所以这种对应关系不具备求导函数的要求。
在微分流形上,函数定义为从流形到实数的光滑映射。而导数在微分流形上的定义是通过切向量和切空间来定义的,而不是通过普通的求导公式。切向量是微分流形上的一种几何对象,它描述了在流形上某一点附近的变化率。
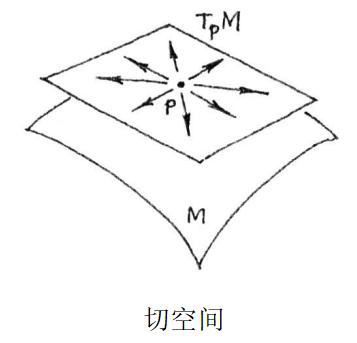
对于多维欧氏空间来说,每一个点都具有若干条切线,流形上的点便可以借助这个概念。
因此,微分流形上的导数是通过切向量来定义的,而不是通过普通的求导公式
素导数与微分,即一个切向量。
将微分流形上的导数转变到切空间以后,由于切向量的基具有函数性质,实际上就是给切向量赋予了坐标系,也就可以求导了。
这个定义确保了导数在微分流形上是局部线性的,并且与流形的局部坐标系无关。

限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。