[遇见君] 这里推荐下面刘瑞祥老师本人的微信号,欢迎各位老师朋友多多关注支持!
最近和一位某小学的数学黄老师讨论最大公约数和最小公倍数,也看了一下对方发来的数学书照片,感觉有几个问题可以说一说。提前说明的是,这里完全以小学数学书里讲的“短除法”为出发点,不涉及“辗转相除法”等内容。
一、用什么例子为好?
对方发来的数学书照片,用的是12和18这两个数,显然不够好:因为这样学生难以判断将来计算的时候用的是侧面的2和3,还是下面的2和3(这里“侧面”指的是短除法提取出来的公约数,“下面”指的是最后各自剩下的因数,下同)。
我开始向那位小学老师建议用30和42,后来再一思索,感觉用24和30更好:
为什么?因为这样一来,不但侧面和底面的数完全不同,容易区别,而且这里底下有一个合数4,这就区分开了“分解质因数”和“求最大公约数最小公倍数”在分解方面的要求:分解质因数要求是分到不能再分为止,最后要求剩下的是质数,但求最大公约数最小公倍数要求最后两个数没有公约数即可,至于剩下的是不是质数,是没有关系的。当然具体到这里的例子最大公约数,是最后剩下的有且只有一个质数。
二、算理是什么?
为什么短除法可以计算最大公约数和最小公倍数?这是个好问题。下面仍以24和30为例,按照短除法的计算方法,显然2和3都是公约数,但最大的呢?当然应该是这两个的乘积,你不可能再往里面添加其它的质因数了,比如你还想再添加个2,这个新的2只是24下面那个4里的因数,不是30下面那个5的因数了。或者可以这样说:
因为24=(2×3)×4,30=(2×3)×5,
所以公共的质数约数只有一个2和一个3,最大公约数是(2×3)。
那么,最小公倍数呢?特别是这位老师问我:为什么侧面的那两个数只需要乘一遍?TA是想说,既然2和3同时是两个数的因数,为什么不能乘两次?(因为类比于底部的数4和5,都只是一个数的约数,乘一遍没有问题,但两个数的公约数,为什么乘一遍)
我的回答是,首先你要承认(2×3)×4×5确实是公倍数,但对方表示不能直接确定,需要进一步计算。我再次解释说:你看这里既有(2×3)×4,也有(2×3)×5,前者是24后者是30,那(2×3)×4×5肯定是前者和后者公共的倍数啊,对不对?对方终于承认我说的有道理。
接下来我问,(2×3)×4×5既然是公倍数,如果再乘个2、3(短除法侧面的数)或者其它大于1的正整数,是不是会变得更大?对方回答说这是肯定的。我想读者也会认可的。
最后最大公约数,(2×3)×4×5一共是4个数,去掉一个可以吗?或者把其中一个换成比较小的数可以吗?显然不行。
结论:(2×3)×4×5是公倍数里最小的,即最小公倍数。
三、三个数或者更多数的最大公约数和最小公倍数怎么算?
当然可以算,但是和前面只有两个数的计算有点区别。我们看怎么算24、30和36的最大公约数和最小公倍数。先看最大公约数:
求最大公约数,要分解到这几个数没有共同的公约数为止,最大公约数是(2×3)=6。
但是求最小公倍数不一样,是按照下面的式子计算的,注意侧面有3个质因数,但是中间那个最后一次没有除以2。
计算最小公倍数一定要分解到任意两个之间都没有公约数,最小公倍数是(2×3×2)×2×5×3=360。
为什么有这个区别呢?因为我们在算最小公倍数的时候,公共的约数只能计算1次,你如果没有最后这一步,那么剩下4、5、6这三个数,而4和6还有公约数2,所以乘得的结果就大了,就不是“最小”公倍数了:(2×3)×4×5×6=720。
四、用韦恩图(圆圈图)表示
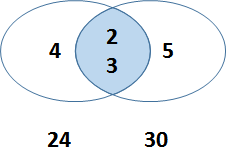
以上是两个数的例子,注意中间的是公共的因子。
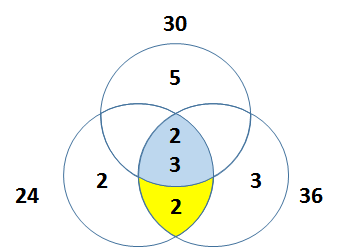
以上是三个数的示意图,注意中间蓝色部分是三个数的公共因子,黄色部分是两个数的公共因子。我希望这两个图能帮助大家理解。
通过几次和小学老师的交流发现,很多时候小学老师困惑的是一些非常琐碎的问题,比如求最小公倍数的时候,如果下面有个1,是不是还需要在最后的乘法式子里写出来?或者如果开始的时候两个数就是互质的,需要侧面写1吗?我想,如果个别老师有这样的困惑可能是老师自身问题,如果大多数老师“说不清楚”,那就是教师培训的问题了,应该有人关注老师们这些具体的困惑,给出一个统一而且合理的解答。
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh