今天在知识星球更新了一部分深度学习信道估计的内容,包含代码及相关文献,想要学习的同学可以加入知识星球。
欢迎加入学术交流Q群:,诸多985/211高校硕博大佬在群内研讨交流,研究方向包含:雷达、通信、RIS、DOA估计、调制识别、故障诊断、雷达通信一体化、侦察干扰一体化、压缩感知、深度学习、强化学习、计算机视觉、图像处理等领域。
相关学习资料见面包多链接。
欢迎加入我的知识星球:,永久获取更多相关资料、代码。
摘要
在这项工作中,我们应用深度学习工具来进行基于下行链路导频的正交频分复用(OFDM)系统的信道估计。具体而言,介绍了一种专门为信道估计设计的基于残差学习的深度神经网络。由于紧凑的网络大小以及底层的网络架构,计算成本可以大大降低。此外,该残余网络架构与任何下行链路导频模式兼容,使其与现代无线系统兼容。在第三代合作伙伴计划(3GPP)信道模型下评估所引入的残差学习方法的估计误差。它优于其他基于深度学习的估计方法,具有与最小均方误差(MMSE)估计性能相当的性能。
索引词-信道估计,OFDM,深度残差学习,图像超分辨率
一、导言
为了支持快速增长的移动的互联网业务量需求,现代无线网络被设计为向用户提供高数据速率。正交频分复用(OFDM)由于其带宽效率和对频率选择性衰落的鲁棒性而被采用为当前4G无线网络中的核心技术,并且仍将是即将到来的5G网络中的关键构建块。在快速变化的无线环境中,获取准确的信道状态信息(CSI)是保证高数据吞吐量的关键。在OFDM系统中信道估计,基于导频的信道估计通常用于获取CSI。更具体地说,发射机发送一种特殊类型的符号,称为导频,其值和位置对于接收机是已知的,接收机通过将接收到的符号与已知的导频信息进行比较来估计信道。在各种估计方法中,最小二乘(LS)和线性最小均方误差(LMMSE)是两种典型的方法。LS方法以其简单性而闻名,然而估计精度通常不令人满意。LMMSE具有很低的估计误差,但它需要二阶信道统计和噪声方差作为先验信息,而且计算复杂度高。
人工智能(AI)在硬件和软件革命性进步的帮助下,在计算机视觉、自然语言处理和游戏等许多领域都表现出了出色的表现。
在无线通信领域,人工智能最近也得到了极大的关注。研究人员已经将人工智能应用于诸如信道估计、符号检测、信道编码、动态频谱共享、资源管理、能量优化、网络故障识别等通信问题。[1]、[2]。
基于深度学习的方法主要集中在信道估计上。在[3]中设计了一个3-隐藏层多层感知器(MLP)用于联合信道估计和解调。在毫米波()大规模多输入多输出(MIMO)系统中,天线数量远大于RF链,[4]提出了一种基于去噪卷积神经网络(DnCNN)的波束空间信道估计方法,这是第一个将计算机视觉工具纳入信道估计的工作。对于基于用户反馈的MIMO下行链路信道估计,[5]引入了基于MLP的方法来替代传统的基于低秩感测的方法。卷积神经网络(CNN)用于学习MMSE信道估计器的参数。在[7]中,信道被视为图像,超分辨率网络(SRCNN)和去噪神经网络(DnCNN)的组合用于信道估计。[8]也将信道视为图像,它修改了[9]中提出的去噪网络来执行信道估计。
在上述方法中,[7]和[8]与我们的工作最相关,因为我们都在OFDM系统中执行导频辅助信道估计,并且将信道估计视为图像处理问题。然而,[8]中的导频必须放置在所有子载波中并且在每个相干持续时间重复,这种导频布置模式与3GPP标准[10]不兼容,而且在快衰落场景中,导频开销巨大。另一方面,虽然[7]支持灵活的导频模式,但神经网络架构并未针对信道估计问题进行优化,因此计算复杂度和估计误差性能需要进一步改善。
受这些因素的激励,在这项工作中,我们引入了一个深度残差信道估计网络()。其结构是优化的信道估计与高性能和低计算成本。除此之外,它支持任何下行链路导频模式,使其与当前无线通信系统兼容。此外,我们的训练机制,使一个训练有素的网络工作在各种情况下,这大大降低了实现的复杂性。
二、问题陈述和常规方法
在正交频分复用(OFDM)系统中,信道被划分为时频网格.在频域中,发送和接收的OFDM符号之间的关系可以表示为
其中X、Y ∈ CNf×Nn是发送和接收的OFDM符号。H ∈ CNf×Nn包含频域中的信道系数,Nf是子载波的数目,Nn是OFDM符号的数目。是乘积(逐元素乘积)。W ∈ CNf×Nn是噪声矩阵,其中每个元素都是均值和方差σ 2w为零的加性高斯白噪声(AWGN)。
通常,导频被稀疏且均匀地放置在时频网格中以用于信道估计目的。在频域中,导频位置处的接收符号Yp ∈ CNpf×Npn可以写为
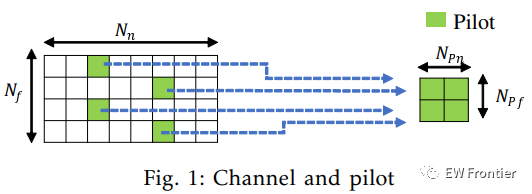
其中Xp ∈ CNpf×Npn是导频符号。如图所示。1,Npf是沿着子载波轴放置的导频符号的数量,Npn是沿着OFDM符号轴放置的导频符号的数量。Hp ∈ CNpf×Npn是导频位置处的信道系数。Wp在飞行员位置为AWGN。
目标是基于Yp和Xp估计H。我们介绍了两种传统的估计方法,最小二乘(LS)估计和线性最小均方误差(LMMSE)估计。
A.LS信道估计
对于LS,通过求解以下优化问题[11]给出导频位置处的估计信道。
其中xp,yp,h p ∈ CNp(Np = Npf ×Npn)是向量化的Xp,Yp,H p。H p是估计的Hp。运算符(·)−1是逆(元素逆)。在非导频位置的信道系数通过二维插值获得,而不需要信道统计和噪声方差的知识。在这项工作中,线性插值应用在LS估计。
B.LMMSE信道估计
在已知二阶信道统计量和噪声方差的情况下,将导频位置的LS估计与滤波矩阵 ∈ CN×Np(N =Nf ×Nn)相乘,得到LMMSE信道估计
滤波器矩阵是通过求解一个最小化问题[11]得到的
其中Rh,hp = E(hhHp)是h和hp之间的互相关矩阵,h是矢量化的H,hp是矢量化的Hp。是导频位置处的信道自相关矩阵。σ 2w是噪声方差。
三、基于深度学习的信道估计
A.单幅图像超分辨率与信道估计
单幅图像超分辨率是计算机视觉领域的一个经典问题,其目标是从单幅低分辨率图像恢复出高分辨率图像。在数学上,它可以表示为
其中Ix是低分辨率图像,Iy是恢复的高分辨率图像,F是以θ为参数的超分辨率模型。
导频辅助信道估计与单图像超分辨率具有类似的问题公式,因此将计算机视觉工具应用于信道估计问题是合理的,受[7]的启发,我们将导频位置H p处的估计信道视为低分辨率图像,并尝试通过该过程将整个信道恢复为高分辨率图像
B.
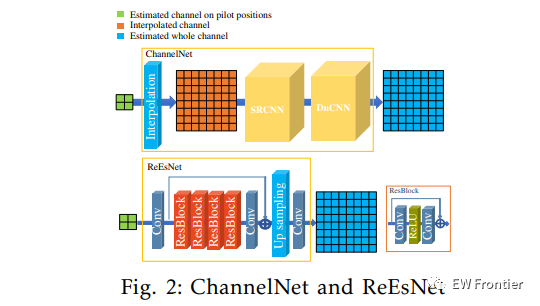
是由[7]提出的用于信道估计的深度神经网络模型。它是两个网络的级联,一个是超分辨率网络SRCNN,另一个是去噪网络DnCNN。估计过程在图1中描绘。2行一,首先通过等式(3)估计导频位置处的信道,接下来将其内插到整个信道的大小(Nf ×Nn),然后内插结果连续地通过SRCNN和DnCNN,最终输出是估计的整个信道。
尽管优于几种近似的LMMSE方法1 [11],但它有几个缺点:1.在程序的第一步进行插值(预上采样),此后的所有计算都在大尺寸输入上执行,因此显著增加了计算成本[12]; 2.插值方法的选择影响最终性能,设计网络时要考虑的超参数; 3.取代端到端训练,SRCNN和DnCNN是分开训练的; 4.网络规模很大,SRCNN和DnCNN组合起来有23个卷积层,总共670 k个参数。
C.最大值深度残差信道估计网络()
残差学习已被广泛应用于图像超分辨率模型中,它不是学习从输入到目标的直接映射,而是学习从输入到残差(输入和目标之间的差异)的映射。好处有两方面:1.通过忽略输入与目标之间的共同信息,该模型可以集中学习高频差异,降低了学习难度,提高了学习效率; 2.它缓解了由深度网络引起的梯度消失问题。受残差学习的优点以及中的超分辨率模型不采用它的事实的启发,我们引入了一种专门为信道估计设计的基于残差学习的神经网络,称为,网络架构如图所示。2排2.网络输入是由等式(3)估计的导频位置处的信道。第一层是一个卷积层,包含16个大小为3 × 3 × 2的滤波器,它将大小为Npf ×Npn ×2的输入H p(复数分为真实的部和虚部,因此最后一个维度为2)映射到大小为Npf ×Npn×16的输出。下面是4个,每个由两个卷积层和一个ReLU层组成,每个卷积层有16个大小为3×3×16的过滤器。旁边是一个卷积层,有16个大小为3×3×16的滤波器,该层的输出大小为Npf ×Npn×16。上采样层将数据大小从Npf ×Npn ×16扩展到Nf ×Nn × 16。最后一个卷积层有2个大小为3×3×16的滤波器,估计的大小为Nf ×Nn ×2的整个信道H Φ是该层的输出。
基于[13]中提出的超分辨率模型进行修改。具体来说,使其对于信道估计有效且高效的条件:1.[13]中的上采样函数被实现为像素混洗层,其只能按相同的因子放大图像高度和宽度。在信道估计中,这等于对导频模式施加Nf Npf = Nn Npn的约束,这是不合适的,因为我们的模型应该适用于任何导频模式。因此,中的上采样功能被实现为转置卷积(又名反卷积)层[14],它可以通过不同的因素放大图像的高度和宽度。2.[13]中的两个超参数,的数量和卷积层中的滤波器数量被设置为32和256,以获得良好的图像超分辨率性能信道估计,这导致一个具有4300万个参数的大型网络。与超分辨率应用中的自然图像(通常包含尖锐边缘)相比,我们的应用中的通道图像相对平滑,降低了学习难度,因此我们相信网络规模可以在不降低性能的情况下压缩。经过一系列实验,这两个超参数最终被设置为4和16。3这是我们可以实现的最紧凑的网络(53k参数),而不会牺牲估计误差性能。
注意,我们采用L1损失而不是广泛使用的L2损失,因为L1损失在我们的实验中显示出更好的性能,4以及其他图像处理问题[12]。
与相比,有几个优势:1.上采样层位于模型的尾部(后上采样),之前的所有计算都是在小尺寸输入上执行的,导致计算复杂度更低,这种架构在最近的超分辨率研究中更受欢迎[12]; 2.上采样层被实现为转置卷积,这是一种可学习的上采样方法,可以被训练以获得最佳权重。3.可以进行端到端的训练; 4.网络的大小被最小化而不降低性能,结果在一个紧凑的网络,只有53 k的参数。
四、实验结果
在该实验中,我们考虑单天线情况,并且将信道大小设置为Nf = 72个子载波和Nn = 14个OFDM符号。信道系数由来自美国三星研究院的链路级仿真器生成,其遵循3GPP城市微(UMi)信道模型[15],中心频率为2.1GHz,信道带宽为20 MHz,包括视线(LOS)和非视线(NLOS)场景。共生成25,000个通道实现,其中60%用于训练,20%用于验证,20%用于测试。
从实践的角度来看,基于深度学习的方法,希望一个经过训练的网络可以适用于各种场景。因此,我们的培训机制是专门设计的(这将我们的工作与其他工作区分开来):1.在生成信道样本时,我们不是对所有样本使用固定的用户速度,而是从0 km/h到50 km/h随机选择; 2.神经网络的训练下的一组信号噪声比(SNR),而不是一个单一的SNR。更具体地,对于每个训练样本,生成不同SNR下的样本的多个版本并用于训练。
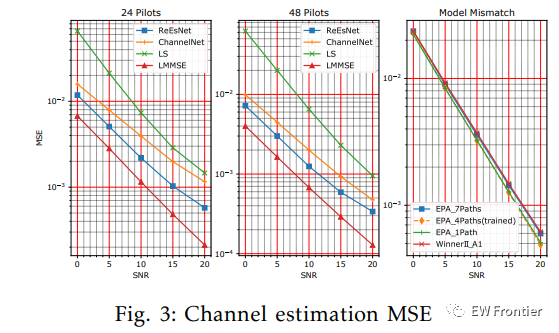
通常,在估计性能和导频数量之间存在折衷。在此评估中,我们将导频数设置为24和48。当使用24个导频时,信道估计均方误差(MSE)如图1所示。3列1用于4种估计方法:、、最小二乘(LS)估计和线性最小均方误差(LMMSE)估计。注意LS仅应用线性插值来估计非导频位置的信道,因此性能在所有4种方法中是最差的。LMMSE需要二阶信道统计量和噪声方差作为先验信息,这在真实的通信系统中是不切实际的,特别是当用户速率变化时,因此其性能被视为一个下界。对于其余两种基于深度学习的方法,不需要信道统计和噪声方差,在低SNR范围内优于,增益为2至3 dB,增益为4至5 dB。对于48个导频的情况,性能如图1所示。3第二列。我们可以看到,随着导频数量的增加,的性能变得越来越接近我们,原因是更高的导频数量降低了超分辨率问题的难度。然而,仍然优于。
在实践中,训练和应用场景之间可能会出现不匹配的情况,因此,测试的健壮性非常重要。在图3中,第三列示出了测试结果(具有24个飞行员),其中在具有4条路径的扩展行人A模型(EPA)下训练,然后在具有7条路径、4条路径、1条路径和模型A1场景(室内)的EPA下进行测试。可以看出,信道模型失配对估计性能没有显著影响。
五.结论
在这项工作中,我们介绍,残差学习为基础的信道估计方法。极具竞争力的估计误差性能,加上紧凑灵活的网络架构,使其成为非常有前途的信道估计方法。对于未来的方向,由于MIMO在当前无线通信系统中的流行,将单天线扩展到多天线情况是重要的。另外,利用连续通道帧的时间相关性并应用递归神经网络可以提高性能,而不是独立地估计每个通道帧,初步结果是有希望的,更多的研究和实验留给未来的工作。
参考文献
[1] R。 , L。 Liu, V。 , H。 Chen, J。 Reed et al。,“ - : A path to -5g and 6g,” arXiv arXiv:1907。07862, 2019。[2] Z。 Zhou, L。 Liu, and H。-H。 Chang, “ for :MIMO-OFDM ,” arXiv arXiv:1907。01516, 2019。[3] H。 Ye, G。 Y。 Li, and B。-H。 Juang, “Power of deep for and in ofdm ,” IEEE 。 Lett。, vol。
7, no。 1, pp。 114–117, 2017。[4] H。 He, C。 Wen, S。 Jin, and G。 Y。 Li, “Deep -based for mimo ,” IEEE 。 Lett。, vol。 7, no。 5, pp。 852–855, Oct 2018。[5] H。 Sun, Z。 Zhao, X。 Fu, and M。 Hong, “ MIMO : From low-rank to deep ,” in 2018 IEEE 19th on SPAWC。 IEEE, 2018, pp。 1–5。[6] D。 , T。 Wiese, and W。 , “ the MMSE ,” IEEE Trans。
。, vol。 66, no。 11,pp。 2905–2917, 2018。[7] M。 , V。 , A。 , and H。 , “Deep -based ,” IEEE 。 Lett。,vol。 23, no。 4, pp。 652–655, April 2019。[8] E。 and J。 G。 , “Deep -based for high- ,” arXiv arXiv:1904。09346, 2019。[9] R。 and P。 Hand, “Deep : image from non- ,” arXiv arXiv:1810。
03982, 2018。[10] 3GPP, “ and ,” (TS) 36。211, 2019, 15。6。0。[11] M。 Simko, C。 Mehlf ˇ uhrer, M。 , and M。 Rupp, “ ¨ with ,” in 2010 ITG WSA。 IEEE, 2010, pp。 251–256。[12] Z。 Wang, J。 Chen, and S。 C。 Hoi, “Deep for image : A ,” arXiv arXiv:1902。06068, 2019。[13] B。 Lim, S。 Son, H。 Kim, S。 Nah, and K。 Mu Lee, “ deep for image super-,” in of the IEEE CVPR , 2017, pp。
136–144。[14] V。 and F。 Visin, “A guide to for deep ,” arXiv arXiv:1603。07285, 2016。[15] 3GPP, “Study on 3D model for LTE,” (TR) 36。873, 2018, 12。7。0。
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh