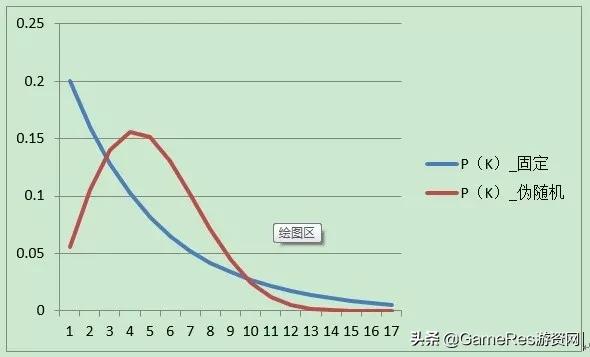
先来一个问题:一机器在良好状态生产合格产品几率是90%,在故障状态生产合格产品几率是30%,机器良好的概率是75%,若一日第一件产品是合格品,那么此日机器良好的概率是多少?
这里需要用到贝叶斯公式,贝叶斯公式一点也不神秘,首先我们要是觉得两个东西之间有关联贝叶斯公式,那么他们就有联合概率
,联合概率可以用链式法则表示
,这个是大家都学过的条件概率,A和B同时发生的概率是B发生的概率乘以B发生下A的条件概率贝叶斯公式,反过来一样成立,所以有:
两边同时除以
,得:
这就是贝叶斯公式。所以贝叶斯公式的范围非常广泛,只要两个东西有关联,能写出联合概率,那么就可以用贝叶斯公式。
机器有良好和故障两种状态,用A表示。产品有合格和不合格两种状态,用B表示。
直接套用公式算一波:
的概率等于:
所以:
看公式是不是很迷惑?下面这个图很清晰:
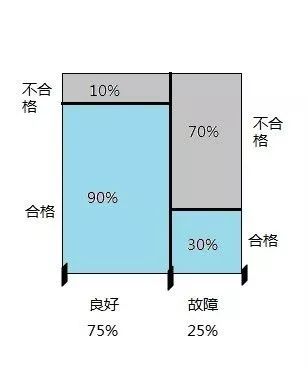
问题要求的机器良好的概率=左下角那个蓝色方格的面积/所有蓝色部分的面积,是不是很好懂?
先验概率是一般情况下机器良好的概率0.75(蓝色面积/总面积),在得知当天有合格产品产出后,灰色面积就没可能了,经过贝叶斯定律的计算后,就得到后验概率0.9(左下角蓝色面积/蓝色总面积)。
贝叶斯公式的扩展:
贝叶斯的公式适用的范围不只是两个事件A和B->
,也可以是参数
和数据data->
,也可以是新闻分类里的贾乃亮和娱乐新闻->
,也可以是垃圾邮件检测里的->
。而随着你学得越多,越会感受到贝叶斯公式的神奇魅力~
END
你点的每个好看,我都认真当成了喜欢
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。