排序算法总结-十大经典排序算法最强总结（下）

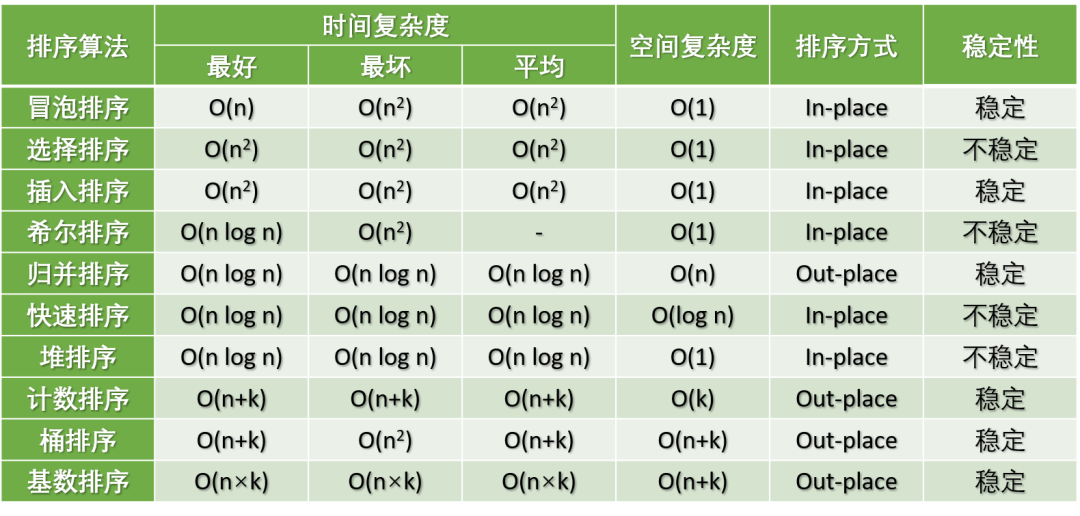
排序问题是一种常见问题，对于一名程序员来说，熟练掌握各种排序算法的特点是至关重要的。我们对五大排序算法的思想、特点和编码（java）进行了总结，这篇文章我们来解决剩下的部分。

归并排序

算法思路

归并排序采用了递归分治的思想，假设初始序列有 n 个元素，则可以看成是 n 个有序的子序列，每个子序列长度为1，然后两两归并，得到 n/2 个长度为2或1的有序子序列，再两两归并，如此重复，直到得到一个长度为 n 的有序序列，这就是归并排序的基本过程。归并排序有两种实现方式，一种是递归，一种是迭代，本文采用递归的方式实现该算法。

最好时间复杂度：O(nlogn)

平均时间复杂度：O(nlogn)

最坏时间复杂度：O(nlogn)

空间复杂度：

递归实现：O(n+logn)，多了递归栈空间大小；

迭代实现：O(n)

稳定性：稳定

算法编码实现

public class MergeSort {
  public static void main(String[] args) {
    int array[] = { 5, 1, 4, 7, 9, 14, 3, 7, 5, 9, 2, 6, 8, 10 };    System.out.println("排序前序列为：");    printArray(array);    mergeSort(array, 0, array.length - 1);    System.out.println("排序后序列为：");    printArray(array);  }
  // 归并排序算法  public static void mergeSort(int array[], int start, int end) {    if (start >= end) {      return;    }
    int mid = (start + end) / 2;
    mergeSort(array, start, mid);    mergeSort(array, mid + 1, end);    merge(array, start, mid, end);  }
  // 归并两个数组  public static void merge(int array[], int start, int mid, int end) {    int temp[] = new int[end - start + 1];
    int i = start;    int j = mid + 1;    int k = 0;
    while (i <= mid && j <= end) {      if (array[i] <= array[j]) {        temp[k++] = array[i++];      } else {        temp[k++] = array[j++];      }    }
    while (i <= mid) {      temp[k++] = array[i++];    }
    while (j <= end) {      temp[k++] = array[j++];    }
    for (int l = 0; l < temp.length; l++) {      array[start + l] = temp[l];    }
  }
  // 打印序列中元素  public static void printArray(int array[]) {    int length = array.length;    for (int i = 0; i < length; i++) {      if (i != length - 1) {        System.out.print(array[i] + " ");      } else {        System.out.println(array[i]);      }    }  }
}

堆排序

算法思路

堆排序采用 “ 堆 ” 这种特殊的结构来进行排序。堆是一个近似二叉树的结构，分为大顶堆（大根堆）和小顶堆（小根堆），通常升序排序采用大顶堆这种结构，大顶堆的含义是其每一个节点的值都不小于其子节点的值，即 V[i] >= V[2i+1] 且 V[i] >= V[2i+2], i = 0, 1, ..., n -1。堆排序的基本思想是，首先通过自底向上的顺序将待排序列建立成一个大顶堆，接着不断地将堆顶元素与最后一个元素交换位置，然后将剩余元素重新构造成一个大顶堆，直至堆的大小为1。

最好时间复杂度：建堆O(n)，第 i 次调整堆需要O(logi)，总共 n-1 次，所以总的是O(nlogn)

平均时间复杂度：O(nlogn)

最坏时间复杂度：O(nlogn)

空间复杂度：O(1)

稳定性：由于元素的比较与交换是跳跃式进行，所以是不稳定的

算法编码实现

public class HeapSort {
  public static void main(String[] args) {
    int array[] = { 5, 1, 4, 7, 9, 14, 3, 7, 5, 9, 2, 6, 8, 10 };    System.out.println("排序前序列为：");    printArray(array);    heapSort(array, array.length);    System.out.println("排序后序列为：");    printArray(array);  }
  // 堆排序算法  public static void heapSort(int array[], int size) {
    if (size <= 1) {      return;    }
    // 建立一个大顶堆    buildHeap(array, size);
    // 调整堆直至堆大小为1    for (int i = size - 1; i > 0; i--) {      swap(array, 0, i);      adjustHeap(array, 0, i - 1);    }
  }
  // 建立大顶堆  public static void buildHeap(int array[], int size) {    for (int i = size / 2; i >= 0; i--) {      adjustHeap(array, i, size - 1);    }  }
  // 调整堆  public static void adjustHeap(int array[], int i, int size) {
    // 左孩子节点下标    int left = 2 * i + 1;    // 右孩子节点下标    int right = 2 * i + 2;    // 选出当前节点与左右孩子节点中的最大值    int max = i;    if (left <= size && array[left] > array[max]) {      max = left;    }    if (right <= size && array[right] > array[max]) {      max = right;    }    // 把当前节点与其最大孩子节点交换，并继续向下递归进行对调整    if (max != i) {      swap(array, i, max);      adjustHeap(array, max, size);    }
  }
  // 交换序列中元素  public static void swap(int array[], int i, int j) {    int temp = array[i];    array[i] = array[j];    array[j] = temp;  }
  // 打印序列中元素  public static void printArray(int array[]) {    int length = array.length;    for (int i = 0; i < length; i++) {      if (i != length - 1) {        System.out.print(array[i] + " ");      } else {        System.out.println(array[i]);      }    }  }
}

计数排序

算法思路

计数排序不是一种比较排序算法排序算法总结，它的时间复杂度可以达到 O(n) ，但使用该排序算法要求待排序列中每一个元素都是0到k区间内的一个整数，其中k为1个整数。其基本思想为对于每一个元素 x ，确定小于 x 的元素个数，利用该信息即可将 x 放到其在输出数组中的位置上去，如果有相同的元素，则要略作修改。具体步骤为首先统计数组array中每个值array[i]出现的次数，存入数组count[array[i]]，接着将数组count中每一项的值等于其与前项相加，则count[array[i]]变为数组array中小于等于array[i]的元素个数，然后填充输出数组，将array[i]放在数组的第count[array[i]]的位置，每放入一个元素将count[array[i]]递减。

最好时间复杂度：O(n+k)

平均时间复杂度：O(n+k)

最坏时间复杂度：O(n+k)

空间复杂度：O(n+k)

稳定性：稳定

算法编码实现

public class CountingSort {
  public static void main(String[] args) {
    int array[] = { 5, 1, 4, 7, 9, 14, 3, 7, 5, 9, 2, 6, 8, 10 };    System.out.println("排序前序列为：");    printArray(array);    countingSort(array, 15);    System.out.println("排序后序列为：");    printArray(array);  }
  // 计数排序算法  public static void countingSort(int array[], int k) {
    int count[] = new int[k];
    //计算每个数字出现的次数    for(int i = 0; i < array.length; i++){      count[array[i]] ++;    }
    //计算小于等于array[i]的元素的个数    for(int i = 1; i < count.length; i++){      count[i] += count[i-1];    }
    //填充输出数组    int output[] = new int [array.length];    for(int i = array.length - 1; i >= 0; i--){      count[array[i]]--;      output[count[array[i]]] = array[i];
    }
    //将输出数组复制回原数组    for(int i = 0 ; i < array.length; i++){      array[i] = output[i];    }
  }
  // 打印序列中元素  public static void printArray(int array[]) {    int length = array.length;    for (int i = 0; i < length; i++) {      if (i != length - 1) {        System.out.print(array[i] + " ");      } else {        System.out.println(array[i]);      }    }  }
}

桶排序

算法思路

桶排序假设输入数据服从均匀分布，首先将待排序列分成m个子区间，也就是m个桶，接着基于一个映射函数f(x)，将待排序列中的每个元素映射到一个桶里，然后对每个桶里的所有元素进行比较排序（如快速排序），最后依次输出桶中的全部元素即可得到一个有序序列。

最好时间复杂度：O(n)，每个元素占一个桶

平均时间复杂度：O(n)，每个桶内元素个数均匀

最坏时间复杂度：O(nlogn)或O(n^2)排序算法总结，只有1个桶，取决于桶内排序方式

空间复杂度：O(n+m)

稳定性：稳定

算法编码实现

import java.util.ArrayList;import java.util.Collections;import java.util.LinkedList;import java.util.List;
public class BucketSort {
  public static void main(String[] args) {
    int array[] = { 35, 21, 44, 87, 69, 14, 3, 57, 15, 59, 20, 46, 78, 10 };    System.out.println("排序前序列为：");    printArray(array);    bucketSort(array);    System.out.println("排序后序列为：");    printArray(array);  }
  // 桶排序算法  public static void bucketSort(int array[]) {
    if (array == null || array.length == 0) {      return;    }
    // 桶数量    int bucketNums = 10;
    // 构造桶    List<List> buckets = new ArrayList<List>();    for (int i = 0; i < bucketNums; i++) {      buckets.add(new LinkedList());    }
    // 将元素划分到每个桶里    for (int i = 0; i < array.length; i++) {      buckets.get(f(array[i])).add(array[i]);    }
    // 对每个桶分别进行排序（快速排序）    for (int i = 0; i < buckets.size(); i++) {      if (!buckets.get(i).isEmpty()) {        Collections.sort(buckets.get(i));      }    }
    // 将排好序的桶中元素赋值回原数组    int k = 0;    for (List bucket : buckets) {      for (int element : bucket) {        array[k++] = element;      }    }
  }
  // 映射函数  public static int f(int x) {    return x / 10;  }
  // 打印序列中元素  public static void printArray(int array[]) {    int length = array.length;    for (int i = 0; i < length; i++) {      if (i != length - 1) {        System.out.print(array[i] + " ");      } else {        System.out.println(array[i]);      }    }  }
}

基数排序

算法思路

基数排序是一种“分配式排序”，基本思想是首先将待排序列中所有的元素统一为同样的数位长度，数位不足的前面补0，然后从最低位开始进行基数为10的基数排序，直到最高位计数排序完成后，序列就会变成有序序列。

最好时间复杂度：O(d(n+k))，d为位数，n为序列长度，k为每一位可能的取值个数。

平均时间复杂度：O(d(n+k))

最坏时间复杂度：O(d(n+k))

空间复杂度：O(d(n+k))

稳定性：稳定

算法编码实现

public class RadixSort {
  public static void main(String[] args) {
    int array[] = { 195, 241, 546, 17, 69, 147, 323, 472, 456, 698, 122, 756, 368, 10 };    System.out.println("排序前序列为：");    printArray(array);    radixSort(array);    System.out.println("排序后序列为：");    printArray(array);  }
  // 基数排序算法  public static void radixSort(int array[]) {    int d = 3;    int k = 10;    for (int i = 1; i <= d; i++) {      countingSort(array, k, i);    }  }
  // 计数排序算法  public static void countingSort(int array[], int k, int d) {
    int count[] = new int[k];
    // 计算每个数字出现的次数    for (int i = 0; i < array.length; i++) {      count[getDigit(array[i], d)]++;    }
    // 计算小于等于array[i]的元素的个数    for (int i = 1; i < count.length; i++) {      count[i] += count[i - 1];    }
    // 填充输出数组    int output[] = new int[array.length];    for (int i = array.length - 1; i >= 0; i--) {      int digit = getDigit(array[i], d);      count[digit]--;      output[count[digit]] = array[i];
    }
    // 将输出数组复制回原数组    for (int i = 0; i < array.length; i++) {      array[i] = output[i];    }
  }
  // 获取元素x的第d位数字  public static int getDigit(int x, int d) {    int radix[] = { 1, 1, 10, 100 };    return (x / radix[d]) % 10;  }
  // 打印序列中元素  public static void printArray(int array[]) {    int length = array.length;    for (int i = 0; i < length; i++) {      if (i != length - 1) {        System.out.print(array[i] + " ");      } else {        System.out.println(array[i]);      }    }  }
}

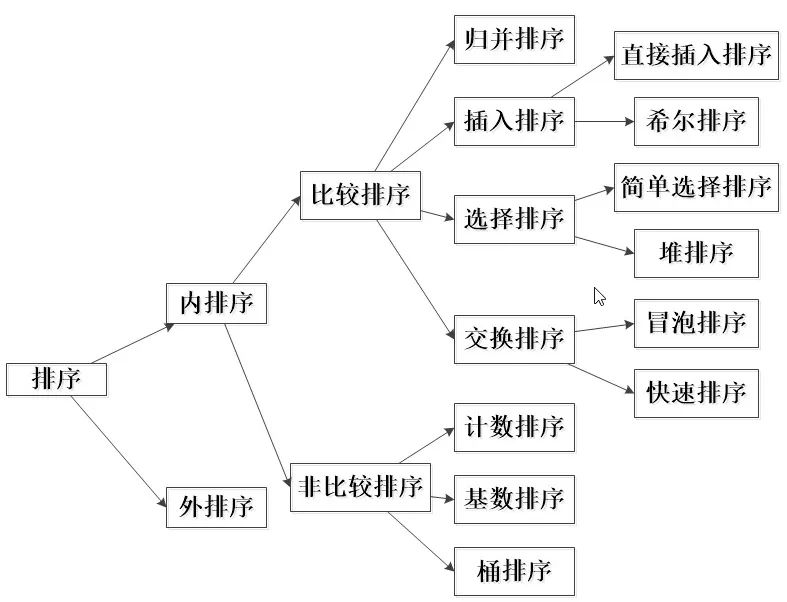
排序算法总结

「作者简介」

严嘉

Gavyn Yan

网易严选后端开发，走在架构师之路上的小白。

网易1024第二届技术马拉松技术极客奖一等奖获奖团队核心成员之一。

目前负责网易严选客服模块相关工作。

限时特惠:本站持续每日更新海量各大内部创业课程，一年会员仅需要98元，全站资源免费下载
点击查看详情

站长微信:Jiucxh