每年高考结束,总会有一种舆论:数学这么难,学生将来的工作生活很少会与数学打交道的,所以国家不用那么重视数学教育,高考干脆取消数学算了。其实这种观点完全错了,错在误会了数学的内容和作用,错在了不了解数学在现代生活中的应用。可以说从人们的衣、食、住、行到卫星导航、人工智能、区块链技术都离不开数学。目前各国不是在弱化数学教育,而是在加强数学教育。
作为一名中学数学老师,想通过做一个系列科普推文,向大家展示一个我们陌生而又熟悉的世界。让大家了解百度搜索、语音识别、密码加密等看似很智能高深的技术,其背后包含的多数人都能明白的简单数学模型。其间我参考了吴军博士的著作《数学之美》和网上一些资源。
我们的这趟旅程从著名的数学问题“哥尼斯堡七桥问题”开始。
01
—
问题的背景
大家都用过百度、谷歌吧?为什么输入一个关键词,就可以在互联网找到有关的所有内容呢?这么神奇,用到什么高科技?其实所有搜索引擎的底层算法都用到了数学的一个分支学科《图论》中的遍历算法。图论是计算机科学中最重要、最有趣的领域,没有之一。大数学家欧拉就是从研究解决“七桥问题”开始创建了《图论》,毫不夸张地说,没有“七桥问题”,就没有互联网。
02
—
“七桥问题”的提出
18世纪初东普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,为方便同行,人们在河上修建了七座桥,把两个岛与河岸联系起来。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。
03
—
解决问题的历程
问题提出后,很多人对此很感兴趣,纷纷到现场进行试验,一时之间还带动了当地的旅游业。但在相当长的时间里,问题始终未能解决。而利用普通数学知识,每座桥均走一次,那这七座桥所有的走法一共有7!=5040种(排列组合),而这么多情况,要一一试验,这将会是很大的工作量。但怎么才能找到成功走过每座桥而不重复的路线呢?于是大家去请教年轻的数学家欧拉。但欧拉当时也没有意识到这是一个数学问题,他也想过使用列举法,列举所有可能的路线,是多少呢?不过欧拉认为这样没有意义,对解决之后同类问题没有参考意义。于是,便在1936年提出将其转化为一个抽象的数学图形模型,将其转化为一笔画问题,这种思维模式就是抽象与符号处理的方法。
04
—
问题的最终解决
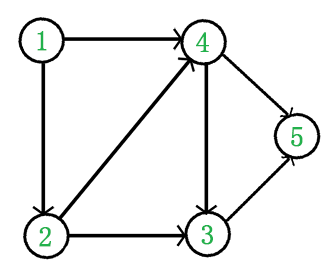
欧拉在研究一段时间之后,将两个对岸与两个小岛这四块陆地抽象为四个点,将通过河流连接四地的七座桥抽象为七条线,将路程这个因素与其他跟过桥无关的要素全部舍弃,于是就将上文的地图抽象为由4个点和7条线组成的下图:
问题至此便被转化为了“一笔画”问题(就是笔不准离开纸,一口气画成整个图形;且每一条线只许画一次,不得重复)。我们将四地分别编号为A、B、C、D,将七座桥用数字1—7来表示。如果从A出发,最后回到A。这个图可以一笔画的话,对于每一个点来说,当画笔沿某条线到达这一点时,必定要沿另一条线离开这点,并且进入这点几次,就要离开这点几次,一进一出,两两配对,所以从这点发出的线必然要是偶数条。因此,一个图形能否一笔画就有了一个判别规则:一个可以一笔画的图形最多只能有两个点(起点和终点)与奇数条线相连。再看抽象图形,图中的四个点都是与奇数条(三条或五条)线相连的,根据判别规则,是不能一笔画的,从而证明了七桥问题所要求的走法是不存在的。
欧拉通过对七桥问题的研究,不仅圆满地回答了哥尼斯堡居民提出的问题七桥问题,而且得到并证明了更为广泛的有关一笔画的三条结论,人们通常称之为欧拉定理。对于一个连通图,通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。欧拉在解答问题的同时,开创了数学的一个新的分支——图论与几何拓扑,也由此展开了数学史上的新历程。
05
—
引发的思考
欧拉的证明与其说是数学证明,还不如看作是一个逻辑证明。一个曾难住那么多人的问题,竟然是这样一个简单的出人意料的推理,还开创了一个新的学科。欧拉非常巧妙的把一个实际问题抽象成一个合适的数学模型,这种研究方法就是我们应该掌握的数学模型方法。这并不需要运用多么深奥的理论,但能想到这一点七桥问题,却是解决问题的关键。
我们的搜索引擎算法要做到简洁高效,当然要“遍历”所有的路径(7座桥),而且不走“回头路”,这不正是和“七桥问题”的解决方案相吻合吗?
大家看,这就是数学应用的惊鸿一瞥。看完此推文,大家还会觉得应该在高考中取消数学吗?欢迎留言。
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh