bp神经网络算法-【预测模型】基于萤火虫算法优化bp神经网络实现数据预测matlab源码

1 算法介绍1.1 萤火虫算法

算法基本思想描述如下：在群体中，每个萤火虫个体被随机分布在目标函数定义的空间中，初始阶段，所有的萤火虫都具有相同的荧光素值和动态决策半径。其中，每个萤火虫个体根据来自动态决策半径内所有邻居萤火虫信号的强弱来决定其移动的方向。萤火虫的动态决策半径会随着在它范围内萤火虫个体的数目而变化bp神经网络算法，每个萤火虫的荧光素也会随着决策半径内萤火虫个体的数目而改变。萤火虫群优化算法是无记忆的，无需目标函数的全局信息和梯度信息，具有计算速度快，调节参数少，易于实现等特点。萤火虫进化过程中，每次迭代都由萤火虫的部署(初始化)、荧光素更新阶段、移动概率计算阶段、位置更新阶段、邻域范围更新阶段五个部分组成，现分别介绍如下：

1、萤火虫的部署(初始化)

2、荧光素更新阶段

3、移动概率计算阶段

4、位置更新阶段

5、邻域范围更新阶段

1.2 bp神经网络1.1 神经网络的结构

神经网络的网络结构由输入层，隐含层，输出层组成。隐含层的个数+输出层的个数=神经网络的层数，也就是说神经网络的层数不包括输入层。下面是一个三层的神经网络，包含了两层隐含层，一个输出层。其中第一层隐含层的节点数为3，第二层的节点数为2，输出层的节点数为1；输入层为样本的两个特征X1,X2.

图1 三层神经网络

在神经网络中每一个节点的都与上一层的所有节点相连，称为全连接。神经网络的上一层输出的数据是下一层的输入数据。在图中的神经网络中，原始的输入数据，通过第一层隐含层的计算得出的输出数据，会传到第二层隐含层。而第二层的输出，又会作为输出层的输入数据。

神经网络中的每一层（除了输入层）都是由神经元组成，也称为节点。每一个神经元都相当于一个感知器。如下图：

图2 单个神经元

在神经网络中，每个节点都将计算出特征矩阵X与权值矩阵的加权和，得到净输入e，然后通过激励函数f(e)得到该节点的输出y。在图1中，每条连线都可以看做是一个权值。

在神经网络中，可以添加输出层节点的个数来解决多分类问题。有四个类别需要分类则，则输出层的节点个数可以设为4个节点，每一个节点代表一个类别。

1.2 BP神经网络的训练过程

神经网络的训练过程分为两个过程：1、向前传播得到预测数据；2、反向传播更新权重。如下图所示：

图3 神经网络的训练过程

第一步、向前传播得到预测数据：向前传播的过程,即数据从输入层输入，经过隐含层，输出层的计算得到预测值，预测值为输出层的输出结果。网络层的输出即，该层中所有节点（神经元）的输出值的集合。我们以图一的神经网络结构为例，分析向前传播过程。

1.得到隐含层的输出y1,y2,y3：

2.获取到第二层的隐含层输出y4,y5，输入的数据也就是第一层隐含层的输出数据y1,y2,y3。

3、通过输出层，得到最后的预测值y。

第二步、反向传播更新权重：根据样本的真实类标，计算模型预测的结果与真实类标的误差。然后将该误差反向传播到各个隐含层。计算出各层的误差，再根据各层的误差，更新权重。

1.计算输出层的误差：其中z为该样本的类标

2计算第二层隐含层的误差

3.计算第一次隐含层的误差：

4、更新权重：新的权值=原权值+学习速率×该节点的误差×激励函数的导函数的值（f(e)的倒数）×与该节点相连的输入值

4.1更新输入层与第一层隐含层之间的权值：

4.2更新第一层隐含层与第二层隐含层之间的权值

4.3更新第二层隐含层与输出层之间的权值

以上就是反向传播的过程。误差从输出层反向的传到输入层，然后再从输入层向前更新权值。

1.3 BP神经网络的设计与实现

（一） BP神经网络的设计

1.设计网络的结构：

本次实验采用java语言实现。设计了包含一个隐含层的神经网络，即一个2层的神经网络。

每层都含有一个一维X特征矩阵即为输入数据，一个二维W权值矩阵bp神经网络算法，一个一维的误差矩阵error，同时该神经网络中还包含了一个一维的目标矩阵，记录样本的真实类标。

X特征矩阵：第一层隐含层的X矩阵的长度为输入层输入数据的特征个数+1，隐含层的X矩阵的长度则是上一层的节点的个数+1，X[0]=1。

W权值矩阵：第一维的长度设计为节点（即神经元）的个数，第二维的长度设计为上一层节点的个数+1；W0为该节点的偏置量

error误差矩阵：数组长度设计为该层的节点个数。

目标矩阵：输出层的节点个数与其一致。

激活函数：采用函数：1/1+e-x

2.神经网络的计算过程

按照以上的设计，向前传播得到下一层的输出结果，如图所示：

求误差过程，如图所示：

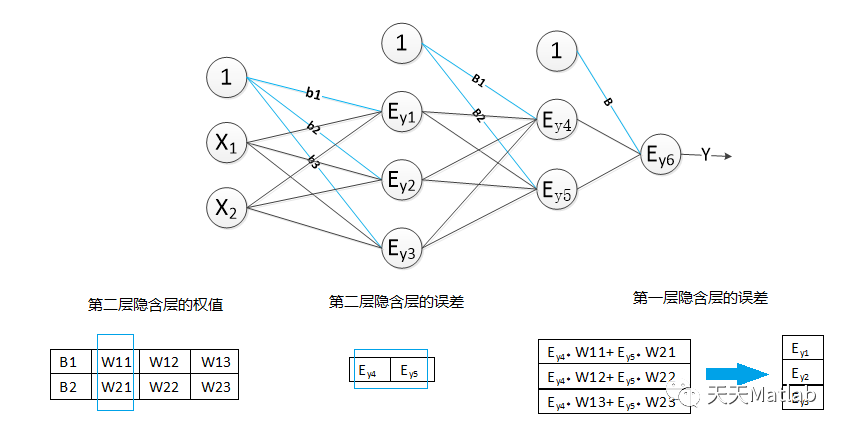
神经网络bp算法应用_bp网络神经算法例题_bp神经网络算法

反向传播过程，调整权值，如图所示：

（二） BP神经网络的实现

一、向前传播得到预测数据：

1.初始化权值 2.训练数据集： 2.1、导入训练数据集和目标值； 2.2、向前传播得到输出值； 2.2.1、获取隐含层的输出 2.2.2、获取输出层的输出二、反向传播更新权重 1、获取输出层的误差； 2、获取隐含层的误差； 3、更新隐含层的权值； 4、更新输出层的权值；

2 部分代码

%% 清空环境
clc
clear

%读取数据
load data 
z=data';
n=length(z);
for i=1:6;
    sample(i,:)=z(i:i+n-6);
end
%训练数据和预测数据
    input_train=sample(1:5,1:1400);
    output_train=sample(6,1:1400);
    input_test=sample(1:5,1401:1483);
    output_test=sample(6,1401:1483);
%节点个数
inputnum=5;
hiddennum=3;
outputnum=1;

%选连样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);

%构建网络
net=newff(inputn,outputn,hiddennum);

d=22;
Lb=zeros(1,d);  % 萤火虫活动范围的下限
Ub=2*ones(1,d); % 萤火虫活动范围的上限
u0=Lb+(Ub-Lb).*rand(1,d);%u0相当于cs的nest(i,:)
para=[20 20 0.25 0.20 1];
[nbest]=ffa_mincon(u0,Lb,Ub,para,inputnum,hiddennum,outputnum,net,inputn,outputn);
x=nbest;

%网络进化参数
net.trainParam.epochs=100;
net.trainParam.lr=0.1;
%net.trainParam.goal=0.00001;

%网络训练
[net,per2]=train(net,inputn,outputn);

%% BP网络预测
%数据归一化
inputn_test=mapminmax('apply',input_test,inputps);
an=sim(net,inputn_test);
test_simu=mapminmax('reverse',an,outputps);
error=test_simu-output_test;
E=mean(abs(error./output_test))
plot(output_test,'b*')
hold on;
plot(test_simu,'-o')
title('结果','fontsize',12)
legend('实际值','预测值')
xlabel('时间')
ylabel('比较')