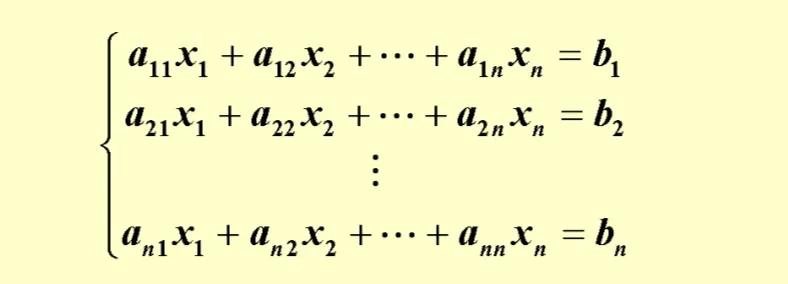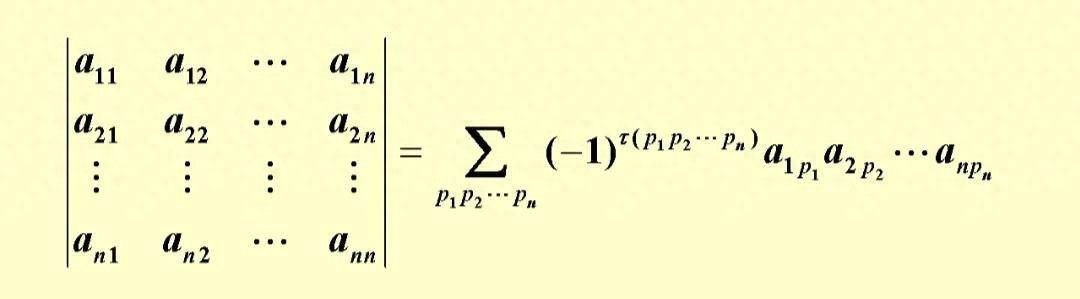雅克比行列式-学好代数，比以往任何时候都更有前景！

同学们好，从线代基础课的第一节导学内容（相当于高数第一讲的预备知识）可以看出，线性代数和高等数学有着完全不同的思维模式。

比如，你要求一个曲边梯形的面积，高等数学会告诉我们，找到f的原函数，用著名的牛顿莱布尼茨公式，算出结果。在高数中，我们已经知道，N-L公式基本上只有理论意义，实际意义不大雅克比行列式，为什么？因为实际问题中原函数几乎是求不出来的（即使能费劲千辛万苦求出来也不是使用数学的任务），那么就要想到泰勒展开式去近似，对吧。

不过，到了代数课里，我们可以理直气壮的说，没有人求原函数，N-L公式根本没用。为什么？因为我们有更秒的办法：你只要给我区间（a，b），给出函数f（比如非负），f的最大值M很容易求得（求导比积分容易的多），我就可以以x=a,x=b,x=M,x=0框出一个矩形区域，在这个矩形里随机产生100万个二维点，相当于一个100万乘以2的矩阵，曲线f下方的随机二维点有多少个，敲几个字母（比如n under f）就知道了，然后用这个n除以100万，再乘以这个矩形面积，就得到曲边梯形面积的近似值了。

现代科技水平处理大量数据的能力，给了我们使用更多新方法的底气和能力。所以，学好代数的意义比以往任何时候都更有前景，学会处理大量数据的基本方法，这是未来工作的关键。

再比如，矩阵承担的任务，至少有三个。

第一，首先是传统意义下的对于系统信息的表达，这个很容易理解和接受；

第二，一个矩阵里，有基准量（基），有表示量（坐标），有了基，就有了一个世界（空间），有了表示量，就有了这个世界里的物种，我们要熟练准确找到基准量和表示量，认识这个世界的样子；

第三，矩阵是一个超级对应法则（变换），它可以基于一个世界，变换出无数个世界，并且可以在不同的世界里穿梭——不同的矩阵，有不同的工作：有的（正交阵）把数据信息做旋转，有的（上下三角阵）把数据信息做剪切，有的（对角阵）把数据信息做伸缩，有的（列矩阵做差）把数据信息做平移，有的（初等阵）把数据信息做镜像，还有的（特殊对称阵）把数据信息做投影，使原空间坍塌……每一个矩阵，都是一个奇妙的戏法。

顺便说一下，在变化过程中，不同世界的度量衡（测度）的改变（想想二重积分换元时的雅克比行列式）可以用行列式的值来刻画，这是现代科技意义下行列式仅有的几个小意义之一。

前面说了，矩阵至少三个任务。那么第四个任务是什么呢？为什么考研代数题一定要考一个(A^T)A？这可不是在讨论题型雅克比行列式，这是矩阵的第四个任务，它全面反应了数据信息之间的相似度，是我们处理大量数据的有利手段，为什么这么说，为什么必考？

那就让我们带着疑问和好奇，开启神奇的代数之旅吧。

行列式的定义_行列式相乘_雅克比行列式