你好贝叶斯公式,欢迎来到《46个知识点》栏目,
我是老编~
书接上文,贝叶斯公式是紧接着全概率公式的又一个公式,上回书说到,全概率公式是计算在好几个“前提”下,某事件发生的概率:
可以看到,全概率公式的这个和式是由n项组成,每一项其实都对应着事件在一个小的“前提”下发生,现在问题来了,如果我知道了事件发生了,那么问你,这个事件是在哪一个“前提”下完成的?这就要用到贝叶斯公式了。
在考研中,全概率公式和贝叶斯公式往往是一起出现,为什么?没有全概率公式,贝叶斯公式将会失去它的载体,也就是说,想用贝叶斯,必须要算全概率,绕不过去贝叶斯公式,所以顺水推舟,两个一起考就是一个最优的选择。
贝叶斯公式:

可以看到,这个式子的分母就是全概率公式。
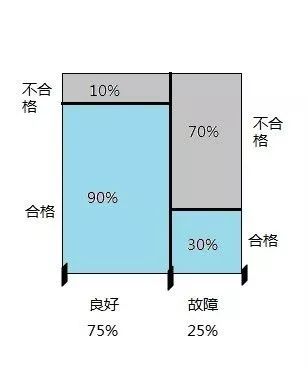
例题,还是昨天的题目
三个箱子中,第一箱装有4个黑球1个白球,第二箱装有3个黑球3个白球,第三箱装有3个黑球5个白球,现任取一箱,再从该箱中任取一球,试求:若取出的是白球,则该球属于第二箱的概率。
昨天已经算出来了,取出的球是白球的概率:

由全概率公式
现在这个事件已经发生,拿着这个结果去找原因“在哪箱中取出来的”就要用贝叶斯了。
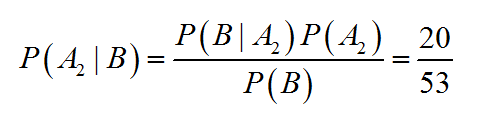
所以,由于贝叶斯“执果寻因”的属性,又被常常叫做逆概率公式。
恭喜你,又学会了一个知识点。
今天是学习的第44/46天,
每天进步一点点,46天带你完成蜕变。
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。