Part 1 前言
各位村友大家好,我们今天为大家带来图的拓扑排序的有关内容。也比较简短,主要就是讲清楚什么是拓扑排序,它怎么实现,以及它有什么样的实际应用场景。
这部分是属于计算机专业性比较强的知识了。如果大家学过离散数学,那么在离散数学中应该对其也会有介绍。
没有关注的小伙伴可以点个关注啦。这样就不会错过我们发的优质的文章啦。
以下是我们本文的思维导图:
我们实际上也就是遵循是什么、为什么,有什么用的方式来去进行讲解。
我们尽可能讲解地简介、清晰。本文的篇幅也不是很多,阅读大概需要7-10分钟。
Part 2 什么是拓扑排序
首先,需要明白,拓扑排序的应用场景是在有向图中。
我们在讲解什么是拓扑排序之前,我们需要了解以下,什么是AOV网,因为拓扑排序大多是应用在AOV网之上的。
什么是AOV网?很简单,顶点表示活动,有向边表示活动的优先关系的有向图叫做顶点表示活动的网络( On )简称为AOV网。
举个例子:
这就是一个AOV网。
在上图中,有向图中的顶点表示活动,而有向边表示活动的优先关系。
那么,人们往往关心一个问题,就是这个AOV网所代表的整个工程能不能顺利地进行。那么拓扑排序,能不能顺利进行的关键就是这些工程能够顺利按部就班地进行,而不是形成了一个环。
那如何判断它能不能顺利进行、不形成环呢?一种方法就是拓扑排序。
那什么是拓扑排序呢?
Part 3拓扑排序的实现
那么,简要地了解了一下拓扑排序是什么之后,我们就需要来去考虑如何实现的问题。
我们老规矩,先是给出基本思路,再来给出代码。
对于一个有向图,拓扑排序是这个样子的:
1)从有向图中选取一个没有前驱的顶点,输出该顶点;
2)删去此顶点以及所有以它为尾的弧;
3)重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。后一种情况说明有向图中存在环。
其实很简单啦。说白了,就是从有向图中一直拿走没有前驱的顶点(和改顶点有关联的边也统统拿走)。如果没有这样的顶点,那就说明有向图存在环。
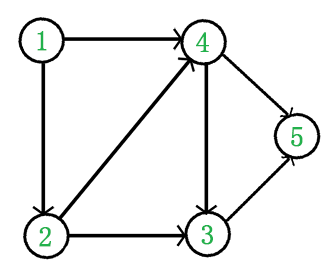
比如下面这个有向图:
首先看,C1和C2没有顶点,随便拿一个。好,假如我拿走了C1,那么有向图就变成了这样:
然后我再拿C2或者是C3都可以,假如我拿C2,那有向图就变成了:
...(如此循环往复)
那么最终,我们拿的顺序就可以是C1、C2、C4、C3、C6、C5、C7。
当然了,顺序有很多,拓扑排序不唯一,只要你一直去拿走没有前驱的顶点就可以了。
思路就是这个思路。是不是很简单?哈哈哈。
那我们在代码中应该如何实现呢?
因为代码可能大家用的不相同,所以我们这里就给出思路和伪代码。这样大家可以用自己熟悉的语言来去轻松实现。
如果我们用邻接表来对图进行存储的话,我们还额外需要两种数据结构,一种是数组,还有一种是一个栈S。
数组我们用来存储顶点入度的数组。那么在删除顶点及以它为尾的弧时,弧头顶点的入度减1。
栈S我们用来暂存所有入度为0的顶点。可以避免重复检测入度为0的顶点。
说到这里想必大家也应该有大致的思路构架了。
我们说下我们的:
Status Topological Sort(ALGraph G){
//有向图G采用邻接表存储结构。若G无回路,
//则输出G的顶点的一个拓扑序列并返回OK,否则返回ERROR
FindInDegree(G,indegree);//对各顶点求入度indegree[0..vexnum-1]
InitStack(S);
for(i=0;i<G.vexnum;++i)//建零入度顶点栈
if(!indegree[i])Push(S,i) //入度为0的顶点进栈
count=0;//对当前输出顶点计数
while (!StackEmpty(S)) {//栈非空,还存在入度为0的顶点 Pop(S,i); //栈顶元素出栈 printf(i,G.vertices[i].data); ++count; //输出i号顶点并计数
for(p=G.vertices[i].firstarc; p; p=p->nextarc){
k=p->adjvex;//对i号顶点的每个邻接点入度减1
if(!(--indegree[k])) Push(S,k); //若入度减为0,则入栈
}//for
}//while
if(count<G.vexnum) return ERROR;//该有向图有回路
else return OK;
}
对有 n 个顶点和 e 条弧的有向图而言,建立顶点入度数组的时间复杂度为O(e);建零入度顶点栈的时间复杂度为O(n);在拓扑排序过程中,若有向图无环,则每个顶点进一次栈,出一次栈,入度减1的操作在 while语句中总共执行e次,所以,总的时间复杂度为O(n+e)。
拓扑排序是不是很简单?实际上,这一节的拓扑排序是我们下一节关键路径的基础。
Part 4拓扑排序的应用
那么,在最后,我们再来说说拓扑排序能有什么实际应用。
实际上,我们刚刚在引出拓扑排序的时候,就有提到过它的应用。我们在这里呢,举一个具体的例子来作证。
如上所示,判断这些课程的先修课是否合理?那就是说看右侧的有向图里是否存在环,在右侧的有向图中,如果A是B的先修课,那么A指向B。那么如果存在环,就有可能存在这样的情况:A是B的先修课、B是C的先修课,C又是A的先修课,那这就修不了了——这种情况就是排课情况不合理。
那我们如何判断右侧的有向图中是否存在环呢?那就是用拓扑排序。
好啦,本节的内容就到此结束啦。如果大家有什么意见欢迎加村长微信,或者留言。同时,没有关注的小伙伴,看到这么用心的文章(不要脸哈哈哈)拓扑排序,能不能给个关注或者点个小赞呢~~
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh