一、定义
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序希尔排序,是直接插入排序算法的一种更高效的改进版本。
希尔排序是非稳定排序算法。
该方法因DL.Shell于1959年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;
随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
二、思路
1、原始数组以下数据元素颜色相同为一组
2、初始增量 gap = /2 = 5,意味着整个数组被分为5组:【8,3】,【9,5】,【1,4】,【7,6】,【2,0】
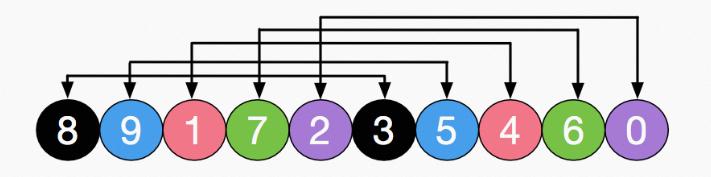
3、对这5组分别进行直接插入排序,结果如下,可以看到,像3,5,6,0这些小元素都被调到前面了,然后缩小增量gap=5/2=2,数组被分为2组:【3,1,0,9,7】,【5,6,8,4,2】

4、对以上2组分别进行直接插入排序,结果如下,可以看到,此时整个数组的有序成都更进一步,再缩小增量gap=2/2=1,此时希尔排序,整个数组为1组【0,2,1,4,3,5,7,6,9,8】,如下

5、此时,仅仅需要对以上数列简单微调,无需大量移动操作即可完成整个数组的排序。

三、代码实现
public static void main(String[] args) {
int[] arr = {7, 6, 9, 3, 1, 5, 2, 4};
shellSort(arr);
for (int i = 0; i 0; gap /= 2) {
//插入排序
//非排序区从gap开始
for (int i = gap; i = gap && arr[j - gap] > tmp; j -= gap) {
arr[j] = arr[j - gap];
}
//将比较元素放入合适位置
arr[j] = tmp;
}
}
}四、复杂度
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:不稳定
冒泡排序:最好时间复杂度为O(n),最坏时间复杂度为O(n^2),平均时间复杂度为O(n^2)。
插入排序:最好时间复杂度为O(n),最坏时间复杂度为O(n^2),平均时间复杂度为O(n^2)。
选择排序:最好、最坏、平均时间复杂度都是O(n^2)。
希尔排序:选择排序的最好时间复杂度为O(n)、最坏时间复杂度都是O(n^2),平均时间复杂度为O(n^1.3)。
从性能来看,当有十万个数据时,直接插入排序 将花费 100亿毫秒,希尔排序 只需要花费170万毫秒。
希尔排序的性能优于直接插入排序,只是属于不稳定排序。
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh