数哲之思
笛卡尔篇(上)
数院×哲院
勒内·笛卡尔是法国哲学家、数学家和科学家,他对现代数学的发展作出了重要的贡献,将几何和代数相结合,创立了“解析几何学”。他也是西方现代哲学思想的奠基人之一,是近代唯心论的开拓者,提出了“普遍怀疑”的主张。
这个春天,复旦大学数学学院将携手复旦大学哲学学院笛卡尔坐标系,分别从数学和哲学的角度,探索笛卡尔的数学巧思与哲学理念,并尝试寻找这两门最古老的学问的共通点与统一性。

笛卡尔的数学巧思

笛卡尔坐标系
代数通常来说是研究数、关系、结构的数学分支,而几何的研究对象则是位置与图形,在坐标这个概念产生以前,代数与几何的研究犹如两座高山被万丈深渊分割。而笛卡尔创立的坐标系巧妙地构建起代数与几何的桥梁,相对位置、图形的大小与形状都可以被两点之间的距离所决定,反之,两点之间的距离亦可以决定图形的大小与形状。
相传,笛卡尔在蜘蛛的启迪下诞生了坐标系的奇思妙想,建立起原点、坐标轴、坐标的相关概念,构建起几何直观与代数抽象之间的联系,将“形”与“数”结合在一起。开创了解析几何学派。笛卡尔坐标系又称直角坐标系,在后人的发展下,又建立起球面坐标系、柱面坐标系、极坐标等实用的坐标系。代数与几何相结合的思想也延续至今,利用抽象代数、交换代数、同调代数研究代数曲线、代数曲面等几何对象的思想形成了代数几何学派。

空间直角坐标系
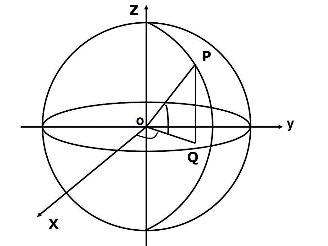
球面坐标系
自直角坐标系创立之起,笛卡尔便启蒙“变量”的概念,几何图形的延伸可以看作坐标的变化,即横纵坐标的变化趋势。笛卡尔将图形的刻画转化为纵坐标关于横坐标的变化关系,通过代数的方程式来描绘直线、曲线、圆、椭圆的性质,为后世“函数”的诞生奠定基础。
回顾高中时期的立体几何与解析几何,便是笛卡尔坐标系的衍生产物,空间立体图形,便是三维坐标构成的集合,椭圆、双曲线等二次曲线与二元二次方程无异。
欧拉-笛卡尔公式
欧拉公式最早是瑞士数学家欧拉于1750年公布的,但后人通过研究笛卡尔的《秘密手记》笛卡尔坐标系,发现早在1635年左右,笛卡尔就已经推导出来这个被称为“欧拉公式”的几何学公式,因此现称为欧拉-笛卡尔公式。这个公式后续衍生出欧拉示性数的概念,给出了曲面的同胚不变量。欧拉-笛卡尔公式表述如下:在任意凸多面体,设V为顶点数,E为棱数,F是面数,则V - E + F = 2。
来看看大十二面体有几个面,几条棱,几个顶点吧,它满足欧拉-笛卡尔公式吗?
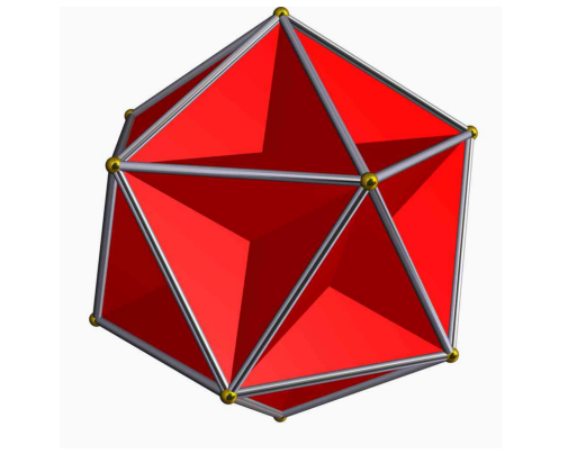
大十二面体
笛卡尔心形线

结语
笛卡尔的数学贡献值得后世铭记,解析几何的建构推动了数学史的发展,变量的思想为微积分的创立奠定基础。笛卡尔是统一代数与几何的数学家,但与此同时他亦是一位“理性主义”哲学家,他的哲学思想指导了他的数学研究,他的数学研究亦推动了他的哲学思考。
在下篇,哲学学院将会采访从事笛卡尔领域研究的佘碧平老师,分享他对于笛卡尔与数哲之思的感受与解读,敬请期待~
文案丨数学科学学院 丁宇哲
排版丨数学科学学院 王祉祺
限时特惠:本站持续每日更新海量各大内部创业课程,一年会员仅需要98元,全站资源免费下载
点击查看详情
站长微信:Jiucxh