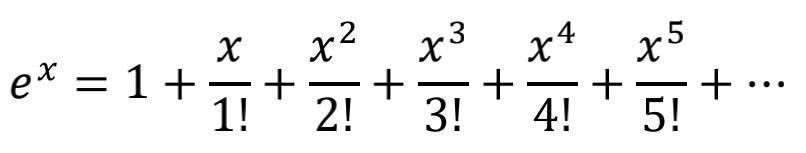1000的阶乘-趣味数学与编程：大整型数字加法、乘法、阶乘

我们知道，计算机内的数据表示只是一个有限字长的二进制序列，表达的十进制整数非常有限：

= 15 (十进制是个2位数，二进制是4位1)

= 255 (十进制是个3位数，二进制是8位1)

= 65535 (十进制是个5位数1000的阶乘，二进制是32位1)

= (十进制是个10位数，二进制是32位1)

(十进制是个20位数1000的阶乘，二进制是64位1)

可以看出，通常一位十进制数需要3.2位二进制数来表示。

相对于整型，数组或字符串可以表示更多的十进制位数，计算时做转换即可。或者链式存储数据块（如一个数据块存储4位数）。

对于浮点数，可以表示更大的数字，但精度有限。

浮点数的位数分为三部分：符号位、阶码、尾码；阶码决定值域，尾码决定精度。

float： 1bit（符号位） 8bits（指数位） （尾数位）

： 1bit（符号位） （指数位） （尾数位）

于是，float的指数范围为-127~+128，而的指数范围为-1023~+1024，并且指数位是按补码的形式来划分的。

其中负指数决定了浮点数所能表达的绝对值最小的非零数；而正指数决定了浮点数所能表达的绝对值最大的数，也即决定了浮点数的取值范围。

float和的精度是由尾数的位数来决定的。浮点数在内存中是按科学计数法来存储的，其整数部分始终是一个隐含着的“1”，由于它是不变的，故不能对精度造成影响。

float：2^23 = ，一共七位，这意味着最多能有7位有效数字，但绝对能保证的为6位，也即float的精度为6~7位有效数字；

：2^52 = 45496，一共16位，同理，的精度为15~16位。（52/3.2≈16）

1 利用链式存储数据块来模拟大整数加数

首先采用一个带有表头结点的环形链来表示一个非负的超大整数，如果从低位开始为每个数字编号，则第1~4 位、第5~8 位……的每4 位组成的数字，依次放在链表的第1 个、第2 个……第n 结点中，不足4 位的最高位存放在链表的最后一个结点中，表头结点的值规定为-1。例如：大整数“”可用如下的带表头结点head 的链表表示。

按照此数据结构，可以从两个表头结点开始，顺序依次对应相加，求出所需要的进位后，代入下一个结点的运算。

#include
#include
#define HUNTHOU 10000
typedef struct node{ 
    int data;
    struct node *next;
}NODE;                                  /*定义链表结构*/
NODE *insert_after(NODE *u,int num);    /*在u结点后插入一个新的NODE，其值为num*/
NODE *addint(NODE *p,NODE *q);          /*完成加法操作返回指向*p+*q结果的指针*/
void printint(NODE *s);
NODE *inputint(void);
void main()
{
    NODE *s1,*s2,*s;
    NODE *inputint(), *addint(), *insert_after();
    puts("*********************************************************");
    puts("*              This program is to calculate             *");
    puts("*       the addition of king sized positive integer.    *");
    puts("*********************************************************");
    printf(" >> Input S1= ");
    s1=inputint();            /*输入被加数*/
    printf(" >> Input S2= ");
    s2=inputint();            /*输入加数*/
    printf(" >> The addition result is as follows.nn");
    printf("    S1= "); printint(s1); putchar('n');    /*显示被加数*/
    printf("    S2= "); printint(s2); putchar('n');    /*显示加数*/
    s=addint(s1,s2);                                    /*求和*/
    printf(" S1+S2="); printint(s); putchar('n');      /*输出结果*/
    printf("nn Press any key to quit...");
    getch();
}
NODE *insert_after(NODE *u,int num)
{
    NODE *v;
    v=(NODE *)malloc(sizeof(NODE));      /*申请一个NODE*/
    v->data=num;                         /*赋值*/
    u->next=v;                           /*在u结点后插入一个NODE*/
    return v;
}
NODE *addint(NODE *p,NODE *q)           /*完成加法操作返回指向*p+*q结果的指针*/
{
    NODE *pp,*qq,*r,*s,*t;
    int total;  // 两数相加的和
    int remain; // total000的结果
    int carry;  // total/10000的结果
    pp=p->next; qq=q->next;
    s=(NODE *)malloc(sizeof(NODE));     /*建立存放和的链表表头*/
    s->data=-1;
    t=s; carry=0;                       /*carry:进位*/
    while(pp->data!=-1&&qq->data!=-1)   /*均不是表头*/
    {
        total=pp->data+qq->data+carry;  /*对应位与前次的进位求和*/
        remain=total%HUNTHOU;           /*求出存入链中部分的数值 */
        carry=total/HUNTHOU;            /*算出进位*/
        t=insert_after(t,remain);       /*将部分和存入s向的链中*/
        pp=pp->next;                    /*分别取后面的加数*/
        qq=qq->next;
    }
    r=(pp->data!=-1)?pp:qq;         /*取尚未自理完毕的链指针*/
    while(r->data!=-1)              /*处理加数中较大的数*/
    {
        total=r->data+carry;        /*与进位相加*/
        remain=total%HUNTHOU;       /*求出存入链中部分的数值*/
        carry=total/HUNTHOU;        /*算出进位*/
        t=insert_after(t,remain);   /*将部分和存入s指向的链中*/
        r=r->next;                  /*取后面的值*/
    }
    if(carry) 
        t=insert_after(t,1);    /*处理最后一次进位*/
    t->next=s;                  /*完成和的链表*/
    return s;                   /*返回指向和的结构指针*/
}
NODE *inputint(void)            /*输入超长正整数*/
{
    NODE *s,*ps,*qs;
    struct remain {
        int num;
        struct remain *np;
    }*p,*q;
    int i,j,k;
    long sum;
    char c;
    p=NULL;                 /*指向输入的整数，链道为整数的最低的个位，链尾为整数的最高位*/
    while((c=getchar())!='n')  /*输入整数，按字符接收数字*/
        if(c>='0'&&cnum=c-'0';       /*存入一位整数*/
            q->np=p;            /*建立指针*/
            p=q;
        }
        s=(NODE *)malloc(sizeof(NODE));
        s->data=-1;             /*建立表求超长正整数的链头*/
        ps=s;
        while(p!=NULL)          /*将接收的临时数据链中的数据转换为所要求的标准形式*/
        {
            sum=0;i=0;k=1;
            while(inum);   
                i++; p=p->np; k=k*10;
            }
            qs=(NODE *)malloc(sizeof(NODE));/*申请空间*/
            qs->data=sum;                   /*赋值，建立链表*/
            ps->next=qs;
            ps=qs;
        }
        ps->next=s;
        return s;
}
void printint(NODE *s)
{
    if(s->next->data!=-1)         /*若不是表头，则输出*/
    {
        printint(s->next);        /*递归输出*/
        if(s->next->next->data==-1)
            printf("%d",s->next->data);
        else{
            int i,k=HUNTHOU;
            for(i=1;inext->data%(k)/(k/10));
        }
    }
}
/*
*********************************************************
*              This program is to calculate             *
*       the addition of king sized positive integer.    *
*********************************************************
 >> Input S1= 1234567890
 >> Input S2= 987654321123456789
 >> The addition result is as follows.
    S1= 1234567890
    S2= 987654321123456789
 S1+S2=987654322358024679
 Press any key to quit...
 */

2 大数相乘

当位数超过整数数据类型的两个大数相乘时，大数可以使用字符串存储，模拟手工做乘法的过程（不同的是，先从高位开始），将每一位相乘的结果先不做进位，累加到一个数组对应下标的元素中，最后做进位处理。

以下是模拟过程：

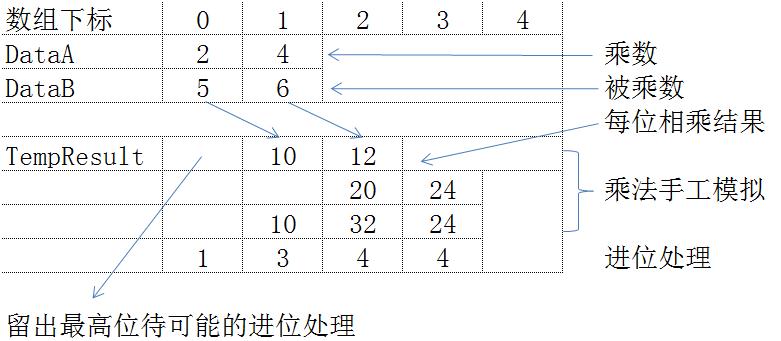
使用双重循环得出[1]＝10，[2]＝32，[3]＝24

数组逐元素逆序迭代处理进位和求余：

    for (i = alen + blen; i >=0; i--) // 处理进位、各数求10的模数，
      //TempResult[alen + blen]是结果的最低位，逆序处理
    {
        if (TempResult[i] >= 10)
        {
            TempResult[i - 1] += TempResult[i] / 10; // i-1位是i位的高位
            TempResult[i] %= 10;
        }
    }

然后将整数数组逐项赋值给字符数组即可。

code:

#include 
#include
#include
// 因为大数过长，所以采用字符串存储， 故要将字符串中字符转化为数字
char *BigDataMutliply(char *DataA, char *DataB)
{ 
    int alen = strlen(DataA); 
    int blen = strlen(DataB); 
    size_t size = sizeof(int)*(alen + blen); 
    int *TempResult = (int *)malloc(size); // 动态数组存储两数各个位相乘的结果
    char *Result = (char *)malloc(sizeof(char)*(alen + blen + 1)); 
    memset(TempResult, 0, size); 
    for (int i=0 ; i<alen; i++) // 从高位开始，迭代出各个位的值存储到数组对应的位
    {
        for (int j=0; j=0; i--) // 处理进位、各数求10的模数
    {
        if (TempResult[i] >= 10)
        {
            TempResult[i - 1] += TempResult[i] / 10; 
            TempResult[i] %= 10;
        }
    }
    i=0;
    while (TempResult[i] == 0)            // 计算数组不包括前导0的位数
        i++; 
    int j;
    for(j=0; i < alen + blen + 1; j++, i++)// 将整数数组转换到字符数组
    { 
        Result[j] = TempResult[i] + '0';
    }
    Result[j-1] = '';                   // 最后位置
    return Result;
}
int main()
{
    char *A = "111111111"; 
    char *B = "111111111";
    char *res = BigDataMutliply(A, B); 
    printf("res = %sn",res);  // 12345678987654321
    system("pause"); 
    return 0;
}

3 大数阶乘

对于一个较小的数的阶乘，较容易通过循环和递归去实现。

对于一个较大的数的阶乘，其结果因为位数较多，基本数据类型无法存储。可以考虑用一个数组a来保存结果的每一位。如计算7的阶乘，模拟过程如下：

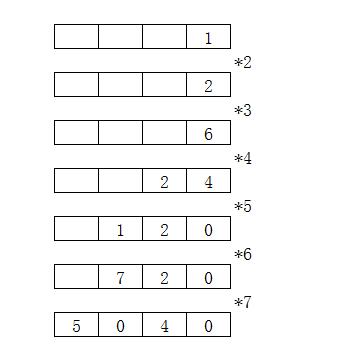
如8!=8*7!=8*5040

a[0] =8*0 = 0

a[1] = 8*a[1]+a[0]/10 = 32

a[0] %= 10 = 0

a[2] = 8*a[2]+a[1]/10 = 3

a[1] %= 10 = 2

a[3] = 8*a[3]+a[2]/10 = 40

a[2] %/10 = 3

a[4] = 8*a[4]+a[3]/10 = 4

a[3] %= 10 = 0

a[4] = 4

// 40320

以a[0]为基准，a[i] = n*a[i] + a[i-1]/10，a[i-1] = a[i-1]逐次迭代。

直接看代码和注释：

#include 
using namespace std;
#define N 10000
long facLoop(int n)  // 循环实现小整数的阶乘
{
    long sum=1;
    for(int i=2; i<=n; i++)
        sum*=i;
    return sum;
}
long facRecur(int n) // 递归实现小整数的阶乘
{
    if(n==0)
        return 1;
    else
        return n*facRecur(n-1);
}
void facBig(int m)
{
    /* 大整数阶乘，使用数组来存储每一位：
    1 初始值a[0]=1；
    2 i=1,2,…,m循环；
    3 j从1开始循环。逐位乘i并加上前一位的进位，并将前一位只保留个位数；
    */
    int a[N]={1};	// a[0]=1，其余各位全为0
    
    for(int i=2; i<=m; i++)				// 阶乘数的循环，如32的阶乘，会连续乘32次
    {
        a[0] *= i;						// 个位做为基准位
        for(int j=1; j<N; j++)          // 整数数组从低位(第2位)开始循环如6!=6*5!=6*120
        {
            a[j] = a[j]*i +a[j-1]/10;	// 逐位乘i并加上前一位的进位
            a[j-1] %=10;				// 前一位只保留个位数
        }
    }
    int n = N-1;
    while(a[n]==0)
        n--;							// 从最高位找到第一个非零数
    cout<<m<<"!有"<<n+1<<"位,"<=0; n--)
        cout<<a[n];
    cout<<""<<endl;
}
int main()
{
    int m;			// 需要计算阶乘的数
    cout<>m;
    cout<<facLoop(m)<<endl;
    cout<<facRecur(m)<<endl;
    facBig(m);
    getchar();getchar();
    return 0;
}
/*
请输入需要计算阶乘的数：12
479001600
479001600
12!有9位,=
479001600
  请输入需要计算阶乘的数：22
  -522715136
  -522715136
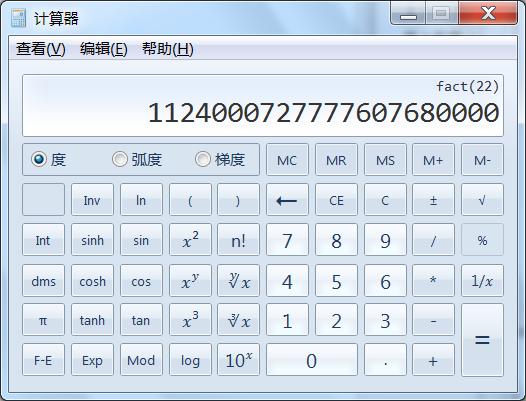
  22!有22位,=
  1124000727777607680000
*/

请输入需要计算阶乘的数：555
0
0
555!有1284位,=
66140856092779467090983316712427699021235319456107896663061009150806651839846293
87085701659314538187743468066779374876229412967164099011221807911833816151991801
33649323135568584492485536333258769584469786383591661922104266566863913614070698
13888154553080852234615605505311576226261267947625648132268820356717111103825491
62857689488683906833874275617940623468544916896330732153487737103632180161575111
81863057926134577070731221701301152592821760868454925199903505386017787199554004
69530073671454816298664788601977137914407564217261944935588590631149093156201859
98321730061506989100813577111773696863103629393244250245849993115399046437308001
89147272918915911770251276375152459026027462464002063813902395684537655374791000
27069982319137060763165525786963451550659008901397431426938167831988871389240730
59060536938650791542851017477232993820261825123659145274388477831568316746298697
33219475045947728356608604070725171727115599864469722301348700056888092787342824
68911323601467977092970083491347570972680751172611060765887478571182355289677008
88379534633760485028152799559579229246893025384153371622056374710987652817622316
17571867644711936978426265600000000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000000000000000000000000000000000
0000

－End－

限时特惠:本站持续每日更新海量各大内部创业课程，一年会员仅需要98元，全站资源免费下载
点击查看详情

站长微信:Jiucxh